Spectro-polarimétrie
par Christian Buil

Cette page présente quelques résultats expérimentaux autour de la mesurer le champ magnétique solaire et stellaire à partir de la signature Zeeman observée dans les spectres. L’effet Zeeman consiste en une division de certaines raies (magnéto-sensibles) en plusieurs composantes. Le détail de cette division est fonction de la nature du champ magnétique, suivant qu’il est dirigé suivant l’axe de visée (champ longitudinal) ou perpendiculairement à celui-ci (champ transversal). Les composantes sont par ailleurs polarisée, circulairement dans le premier cas, linéairement dans le second cas. L’observation de la polarisation des raies spectrales est le moyen indirect utilisé pour déceler à distance le champ magnétique des étoiles.
L’effet Zeeman est en général difficile à observer, même dans la situation favorable des étoiles magnétique du type Ap/Bp. L’empreinte spectrale d’un champ magnétique de 1 kG (1000 Gauss), déjà conséquent en soit, correspond à une séparation des raies qui n’est que d’une petite fraction d’angströms. Un champ équivalent peut être mesurer dans les taches solaire, comme je le montre aussi dans cette page.
Pour des raisons techniques et compte tenu de l’ampleur des phénomènes, le champ longitudinal <Bz> est le plus facile à mesurer. En sa présence, les raies spectrales sont dédoublées avec une séparation en longueur d’onde des deux composantes par rapport à la longueur d’onde nominale, telle que :

Dans cette formule les longueur d’onde s’expriment en angströms et le champ en magnétique en Gauss. Le coefficient g est le facteur de Landé. Celui-ci fixe la sensibilité de la raie étudiée au champ magnétique. Les valeurs de ce facteur sont comprises entre 0 et 3 suivant la nature de la transition responsable de la raie. En plus de s’écarter en longueur d’onde, les deux composantes Zeeman en question sont polarisée circulairement, avec un sens de rotation droit pour l’une et gauche pour l’autre.
L’observation de la polarisation droite et gauche dans le profil des raies spectrales est un moyen efficace pour mesurer un écartement Zeeman (et donc le champ magnétique, ici longitudinal) d’amplitude plus petite que la largeur apparente des raies (leur FWHM, fonction de la largeur effective des raies et aussi du pouvoir de résolution du spectrographe).

Le dispositif de mesure est relativement simple ici (voir le schéma dessus : on positionne à l’avant de la fente du spectrographe (ou de la fibre optique) un polariseur linéaire fixe et une lame de phase (ou lame à retard) du type quart d’onde, dont l’axe rapide peut être tourné de +/-45° par rapport à l’axe passant du polariseur. Suivant que l’axe de la lame quart d’onde est à -45° ou +45° lors de la prise du spectre, on isole la polarisation circulaire droite ou gauche. Il faut donc réaliser deux spectres au minimum. Cet ensemble expérimental constitue un polarimètre élémentaire.

Ci-dessus, la réalisation effective d’un analyseur de polarisation. L’équipement se fixe par le coté gauche au télescope via un coulant de 50 mm, alors le spectrographe est fixé sur le coté droit par un coulant du même type. La lumière rencontre d’abord la lame quart d’onde que l’on peut actionner par un levier rotatif d’amplitude de +/-45°. Le polariseur rectiligne fixe fait suite dans ce montage et dans le sens de propagation de la lumière. Le dispositif est simple d’usage et efficace car le fait d’actionner le levier ne modifie quasiment pas la configuration instrumentale entre les deux mesures à +/- 45°, qui sont donc très cohérentes entre-elles. Ce ne serait pas du tout le cas s’il fallait par exemple désolidariser le spectrophraphe du télescope à chaque manoeuvre, ce qu’il faut absolument éviter de faire.
J’ai utilisé pour cette expérience des éléments polariseur économiques : le polariseur et la lame de phase sont constitués de supports en acétate minces (quelques dixièmes de millimètre), que l’on peu découper à la taille voulue au ciseau. Ces composants sont disponibles au catalogue Edmund Optics (référence 88251 pour le retardateur 1/4 d’onde, référence 86186 pour le polariseur).
Les simulations de l’effet Zeeman ci-contre montrent les deux profils de raies observée suivant que l’on isole les polarisations circulaires droite ou gauche. La somme de ces profils (notés IL et Ir) est le profil de Stokes I (l’aspect de la raie tel qu’il serait vu sans polarimètre).

L’écartement entre les deux profils IL et Ir donne une mesure directe de la force du champ longitudinal (voir la formule ci-avant). Cet écartement est cependant souvent plus petit que le FWHM des raies (largeur à mi-hauteur), d’où la nécessité de passer par la mesure de la polarisation pour l’évaluer.

Le résultat de la différence des profils de raie IL et Ir est proportionnel au spectre de Stokes V, indicatif du taux de polarisation circulaire (et du signe de cette polarisation) dans le profil, comme l’indique la simulation à gauche. Sous sa forme normalisée, l’expression du profil de Stokes V pour les champs modérés est :


Commençons par déceler le champ magnétique au niveau des taches solaire de notre Soleil. Celle cible est commode car éclatante et car les taches solaire sont associées à un champ magnétique significatif.
L’observation a été réalisé le 15 octobre 2016 en profitant de la présence d’un petit groupe de tache (voir l’image à droite, prise avec le caméra de guidage de la bonnette à fibre eShel). On réalise d’abord des spectres de la région notée A, c’est-à-dire le centre de la tache solaire principale du groupe actif, l’endroit où règne un champ magnétique maximal. Le petit cercle en haut en gauche de l’image représente la zone d’analyse (coeur d’une fibre optique de 50 microns).


Le télescope type Celestron et le spectrographe VHIRES-MO (R=48 000 - cliquer ici pour des détails). Une fibre fait l’interface entre le télescope et le spectrographe. J’utilise une bonnette eShel coté télescope. La section polarimétrique (filtre polariseur fixe et lame 1/4 d’onde mobile en rotation) est disposée dans le coulant de 50 mm, un peu à l’avant de la fibre.
Les graphiques ci-après montrent une portion du spectre de la tache vers 4700 A, avec de haut en bas, les profils IL et Ir réalisés à la suite en lumière polarisée circulaire gauche et droite respectivement (courbes rouge et bleu), puis le profil de Stokes I/Ic, puis enfin le profil de Stoke V/Ic (donc, la mesure du degré de polarisation circulaire intégré dans l’image de la tache, ici avec un taux atteignant jusqu’à 5 ou 6%).

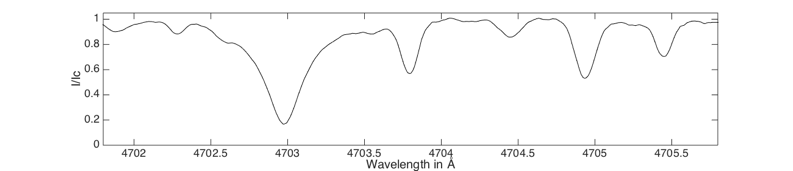

Le dédoublement Zeeman de la raie Fe I 4704,8 A, dont le facteur de Landé est particulièrement élevé (valeur indiquée dans la parenthèse, ici g = 2,59), est immédiatement visible lorsqu’on superpose les profils spectraux correspondant aux polarisation gauche et droite. L’écartement mesuré entre les deux composantes Zeeman est de 0,0278 +/- 0,0020 A. On en déduit que champ longitudinal dans notre modeste tache solaire au moment de l’observation est <Bz> = 535 +/- 30 Gauss.
Pour démontrer que l’on observe bien le champ magnétique, le spectre du point B indiqué dans l’image de la surface solaire est réalisé. Dans cette zone, loin d’un centre actif, le champ magnétique est supposé très faible, sinon quasi nul à la précision visée. Les graphes ci-après confirment ce résultat.


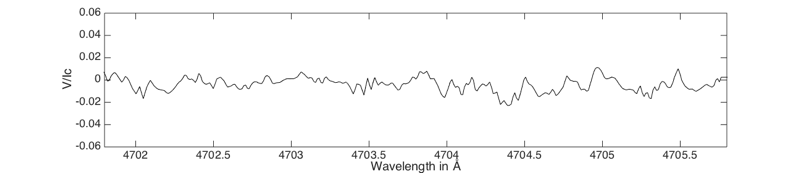
A présent le dédoublement de la raie Fe I 4704,9 A est infime, ce qui confirme que le champ magnétique dans le zone B est très faible. Le profil V/Ic donne une idée de l’erreur de mesure de la polarisation circulaire, ici +/-0,6 %.

Réglage « visuel » des éléments du polarimètre. Le filtre PLC est un filtre polarisant photographique standard, dit « circulaire » (assemblage d’un filtre linéaire et d’une lame 1/4 d’onde). Ce composant est utilisé ici pour générer un état de lumière polarisée circulaire lors des tests et ce, à peu de frais.

Voici à présent le rapport d’observation du champ magnétique de l’étoile Ap, α2 CVn (Cor Corali), l’une des étoiles magnétique les plus brillante du ciel. La mesure à partir du profil des raies métalliques demeure cependant un sujet difficile, un challenge pour les amateurs. La détection demande un spectrographe disposant d’un haut pouvoir résolvant (R = 30000 ou plus idéalement) et des spectres acquis avec un haut rapport signal sur bruit. Un bon télescope de 400 à 500 mm de diamètre au moins et l’usage d’un spectrographe bien stable sont des conditions à réunir pour réussir. Pour cette observation j’emploie un télescope C11 (D=280 mm) et un spectrographe VHIRES-MO.


Allure caractéristique d’un spectre 2D VHIRES-MO, celui de la lumière solaire (noter la troncature des ordres à gauche et à droite).
La raie rouge de l’hydrogène de l’étoile Véga. Comparaison entre un spectre VHIRES-MO et un spectre ELODIE (archive OHP).
Une fois une paire de spectre réalisé, en isolant successivement les polarisation circulaire gauche (L) et droite (R), on calcule le spectre de cette polarisation en faisant ;

Afin de réduire l’effet négatif d’éventuelles dérives temporelles durant cette acquisition séquentielle (par exemple le fait que la hauteur de l’étoile au dessus de l’horizon change en cours d’observation), on préfère réaliser une séquence de mesure LRR’L’ que l’on traite de la manière suivante :

On en profite pour calculer un spectre dit « à polarisation nulle » en combinant la séquence de mesures de cette manière :

Un écart à la valeur nulle dans ce dernier spectre permet de juger l’erreur de mesure (idéalement, sans faute de mesure et en absence de bruit, ce spectre doit être plat).
Ci-après, le résultat des mesures de l’étoile Cor Corali sur la raie Hα réalisées entre le 11 mars 2017 et le 8 avril 2017 depuis mon observatoire personnel de Castanet-Tolosan, région Toulousaine (télescope de 0.28 cm + spectrographe VHIRES-MO R=48000). L’éphéméride de la phase adoptée est JD = 2419869.720 + 5.46939 x E, une formule qui indique que le période de rotation de l’étoile est de 5,46 jours environ.

Ce résultat constitue s’en doute la première mesure du champ magnétique d’une étoile avec des moyens amateurs. Il apparait en effet que la polarisation circulaire dans la lumière de la raie de l’hydrogène est détectée sans ambiguïté (composante V du paramètre de Stokes). Par ailleurs, le critère de polarisation nulle (N) n’indique pas la présence de biais instrumentaux très significatifs, ce qui consolide le résultat (des artéfacts sont seulement remarqués au niveau des raies telluriques H2O - on rappelle à ce propos que l’observation est réalisée depuis un observatoire de plaine avec une atmosphère pas particulièrement sèche). Le cycle de rotation de l’étoile est aussi bien mis en évidence. Le temps total effectif d’observation pour chaque date est de 45 minutes environ.
L’illustration suivante concerne la mesure sur une raie métallique, associée au Cr II, avec à gauche le spectre du paramètre de Stokes I (spectre classique de l’objet), au centre le spectre de Stokes V (polarisation circulaire) et tout à gauche, un extrait d’une publication de O. Kochukhov & all (A&A 513, A13, 2010) concernant cette même étoile (j’ai adopté la même origine pour la phase).

L’accord entre les données professionnelle et amateur est très bon, ce qui valide la procédure employée et le potentiel des amateurs dans un domaine aussi pointu que la spectropolarimétrie. On remarque ici que le profil des raies en intensité (Stoke I) change avec la phase (en fonction de la rotation de l’étoile autour de son axe), ce qui indique la présence de gigantesques tâches à la surface de l’étoile. Mais comme le spectre ne varie pas de la même manière suivant la raie considérée, il apparait qu’il s’agit de taches liées à des concentrations chimiques différentes à la surface de l’étoile ! On trouve des taches de chrome, d’europium… que l’on peut cartographie en 3D (imagerie Doppler). Ces structures sont quasi permanentes dans le temps. De même, le champs magnétique n’est pas identique en tout point du disque du fait de la structure de ce champ et aussi de l’inclinaison particulière du pôle de rotation de l’étoile et de son pôle magnétique ‘(certaines étoiles possèdent plusieurs pôles magnétiques !). Ce champ est dit « fossile », car capturé au moment où c’est formée l’étoile. Tout comme la surface tachée, l’aspect en 3 dimensions de ce champ peut être cartographier (imagerie Zeeman), comme l’indique l’illustration, adaptée avec des données de l’article de O. Kochukhov déjà cité.

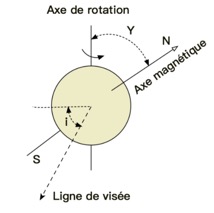
Le modèle du « rotateur oblique ». Les axes de rotation et du dipôle magnétique ne sont pas confondus, ce qui provoque une variation périodique du champ magnétique apparent, mis en évidence par l’étude de l’effet Zeeman sur les raies spectrales.
Un spectrographe « standard » ne mesure que l’intensité I de la lumière. Ce faisant on laisse de coté les 3/4 de l’information que cette dernière contient, les paramètres de Stokes Q, U, V, les deux premiers ayant trait à la polarisation rectiligne de l’onde, le dernier concernant la polarisation circulaire. Certes cette information est bien cachée - nos détecteurs n’y sont pas directement sensible, mais elle est accessible aux amateurs avec un peu de méthode. S’attaquer à ce sujet est une nouvelle aventure pour nous.
L’enjeu astrophysique pour les professionnels est d’importance, il s’agit d’étudier les mécanismes du magnétisme stellaire. Pour les amateurs, la tâche est techniquement ardue : nous sommes en limite des capacités, notamment quant on s’attaque comme ici à l’extraction du subtil spectre de Stokes V des raies métalliques (ce qui demande un haut pouvoir résolvant et d’un fort rapport signal sur bruit, deux exigences contradictoires). La difficulté est relâchée en travaillant sur les raies de l’hydrogène (série de Balmer) des étoiles chaudes car la signature Zeeman peut alors être mise en évidence avec des spectrographes dont le pouvoir de résolution est relativement modeste (R=2000 typiquement - voir S. Bagnulo et all, Astronomy and Astrophysics, 389, 191, 2002 ou encore Bagnulo et all, ESO Messenger, 104, 32-36, 2001) : c’est mon prochain domaine d’investigation et peut être le votre aussi….
Une liste d’étoiles Ap/Bp brillantes sur lesquelles ont peut mesurer la présence d’un champ magnétique :


Comme on l’a vu au début de cette page, le champ magnétique au travers de sa signature Zeeman peut être mesuré à la surface de notre Soleil. Il est possible de réaliser des images de ce champ, que l’on appelle magnétogrammes. La procédure est fort semblable à celle employée pour les étoiles, sauf qu’ici on réalise une image en 2D directe de la surface de l’astre. Pour l’exemple ci-après, j’ai utilisé une version « boosté » du spectrographe LHIRES III (fente très étroite de 9 microns et faisceau très fermé). Deux images successives pour l’une et l’autre orientation de la lame quart d’onde sont obtenues ligne après ligne (techniques du scan avec défilement continu du Soleil sur la fente d’entée et reconstruction du disque à posteriori en mettant les lignes cote à cote).


Tout autre chose que la mesure du champ magnétique : la mesure de la polarisation à haute résolution spectrale peut servir à sonder la présence d’enveloppes de poussières autour de certaines étoiles, comme dans le cas de l’étoile post-AGB 89 Her. On mesure à présent la polarisation linéaire (vecteur de Stokes Q et U, puis le taux de polarisation P qui en résulte). Le télescope employé est un Celestron 11, le spectrographe est le VHIRES-MO (R= 48000) et l’analyseur un simple filtre PLC de photographe ne coutant que quelques dizaines d’euro. Ce dernier est un analyseur de la polarisation rectiligne. On réalise 4 mesures avec un pas angulaire de 45° de l’axe du filtre, ensuite combinées pour calculer le taux de polarisation rectiligne de la lumière de l’astre.

