18. CHARACTERIZATION OF THE LINE PROFILE
Some astrophysical parameters can be extracted from a spectrum by the measurement of the spectral line profile. For example the measurement of the profile gives access to the temperature of surface of a star, at its disk speed, at the speed of expansion of gases, at the pressure, etc. Many quantities are often given: the equivalent width of the line, the line FWHM, the FWZI, the V/R ratio and the peak intensity.
Equivalent Width (W) is defined as the section of a surface counted between the level of the continuum, normalized to unity, and reference zero, having a surface identical to the profile of line (see figure below). The equivalent width is thus measured in wavelength unit (in angstroms for example). Sometimes the normalized equivalent width Wl is used, which is the equivalent width W divided by the wavelength of the line, which is useful to compare the shape of lines located at different wavelengths.
Mathematically we have:
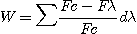
with Fc=1 the continuum level unit normalized, Fl the line profile level, and dl the sampling in wavelength unit. Note that W>1 for an absorption line and W<1 for an emission line.
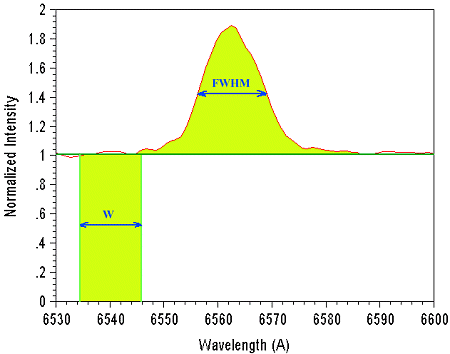
Equivalent Width and Full Width at Half Maximum definitions (H-alpha profile of the Be star 59 Cyg).
A problem is when for example an emission line is superimposed on a large photospheric absorption line (it is often the case with Be stars - see bottom of this page). If W is the measured total equivalent width (emission + absorption) and if Wph is the equivalent width of the photospheric line, the true equivalent width We of the emission line is:
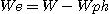
The true difficulty is here to know Wph which is often deduced starting from a theoretical profile of photospheric line or from interpolation of observational data.
Full Width at Half Maximum (FWHM) is the width measured at half level between the continuum and the peak of the line. The FWHM is expressed either in wavelength unit or in speed unit when the objective is to measure expansion or disk speeds (if FWHM is in unit of wavelength, the width in km/sec is given by c . FWHM /l, with c is the speed of the light = 3.105 km/s). Example, suppose that the FWHM is of 2A at 6563A, the equivalent resolved velocity is about 90 km/s.
Notice that the FWHM measured had to be corrected for instrumental width according to the equation:

FWHMinstrument is the width that one measured on a very fine line. It is also the theoretical spectral resolution of the spectrograph.
Some time the FWZI is defined: the Full Width at Zero Intensity. It is the base width (at continuum level) of broad emission or absorption component lines.
The V/R is useful for the study of Be-stars. Often for these stars a central intensity minima divide emission into a Violet (V, at shorter wavelength) and a Red (R, at the long wavelength side) component. Relative intensities of these two components, V/R, measured from the continuum, check the asymmetries of the observed profile. Asymmetries are sometime also observed in single emission lines. In this case if V>R the violet flank is steeper than the red one and if R>V the reverse is found. Note that R>V is produced by expanding motion and V>R by contracting motion.
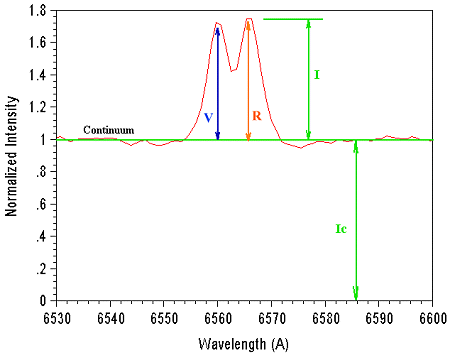
V/R and I/Ic definitions (H-alpha profile of the Be star 4 Crb).
The peak intensity (P) is the ratio between the intensity at the center of the line I and the intensity of the continuum Ic:
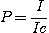
It should be noticed that these definitions remain valid if the line is in emission or absorption compared to the continuum. It will be still noted also that the precision of the estimation of these parameters requires a good accuracy on the level of continuum, that implies the photometric procedures of calibration that we saw previously.
In the case of double pic Be stars, an useful parameters often given, is the peak separation DVpeak (in km/sec).
It is also possible to derive the projected rotational velocity (V.sin i) of Be stars using the FWHM value of an isolated and relatively quiet nearly photospheric line, i.e. a line less affected by the emission and/or absorption produced by the circumstellar enveloppes (He I at 6678 angstroms is some time a good line in the case of my survey). Under the assumption of a Gaussian profiles for this line the V.sin i valeur is computed using the following formula:
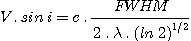
where l is the laboratory wavelength of the line, c is the velocity of light and FWHM given in unit of wavelength.
A derived parameter from the preceding informations is the radii of the emission disk in the case of Be stars studies (Keplerian rotation of the disk hypothesis):
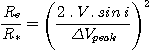
where Re is the radius of the emission disk and R* is the photospheric radius of the star.
For the situation of a weak emission feature into an absorption photospheric line it is useful to subtract this photospheric profile before equivalent width calculation. We use the following empirical formulae for fitting the photospheric profile P(l) (see J. Chauville & all, A&A, 378, 861-882, 2001):
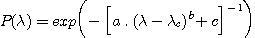
where lc is the central wavelength of the observed
profile and where a, b, c are constants which are determined interactively
and graphically under VisualSpec.
For the example below (17 Tau star)
the computed parameter values are:
a=0.042, b=2.30,
c=2.80, lc=6563.4
A
Notice the revealed effective circumstellar emission (green curve) after subtraction of the photospheric computed profile to the observed spectrum (bleue curve). The measured equivalent width is here of 0.49 angstroms.
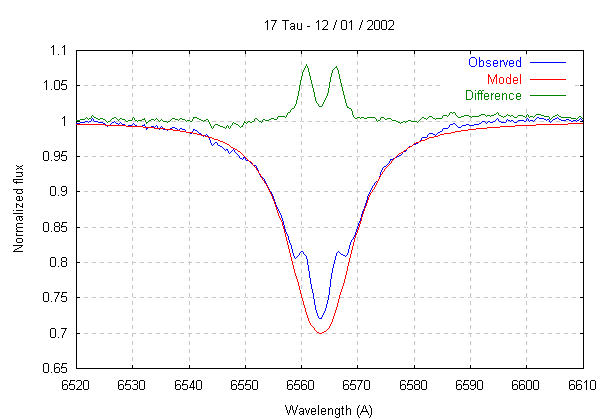
Fitting procedure of a photospheric
line profile. The observed spectrum is in bleue. The fitted model
is in red.