
D en radians
h = altitude en kilomètres
r = rayon terrestre (~ 6368 km)
Vous trouverez à partir de cette page des explications et des formules de calcul sur :
|
|
D en radians h = altitude en kilomètres r = rayon terrestre (~ 6368 km) |
Cette formule intègre des éléments de réfraction. Il n'est donc pas possible d'en déduire directement la distance à l'horizon par la trigonométrie.

|
distance en km h = altitude en mètres |
Cette formule est approximative, mais elle intègre aussi la réfraction (sans la réfraction, la constante serait 3,57 et non pas 3,8). La précision est de quelques %.
calcul de l'azimut, de la distance et de la ligne de visée
J'ai réalisé des calculs différents de ceux que Michel APERIO présente sur son site, quoique appliqués au même triangle Canigou - centre de la Terre - point d'observation.
J'ai effectué au préalable un travail le plus précis possible de relevé de positions géographiques (MAJ 19/04/2020 : en 1999, il n'existait pas Google Maps pour obtenir instantanément les coordonnés d'un lieu !). J'ai utilisé pour cela le quadrillage kilométrique Lambert III sur les cartes IGN, permettant d'avoir un positionnement au mm près, soit 25 m sur le terrain (sauf Notre-Dame de la Garde et le Rove). Dans le cas du Canigou, j'ai doublé ces relevés avec le quadrillage UTM fuseau 31 qui est reporté sur la dernière édition de la carte. Puis j'ai effectué les conversions vers les coordonnées polaires à l'aide du logiciel PathFinder (traitement de levés GPS). Des divergences peuvent apparaître avec d'autres relevés, mais cette méthode a l'avantage de se baser sur un seul système géodésique homogène.
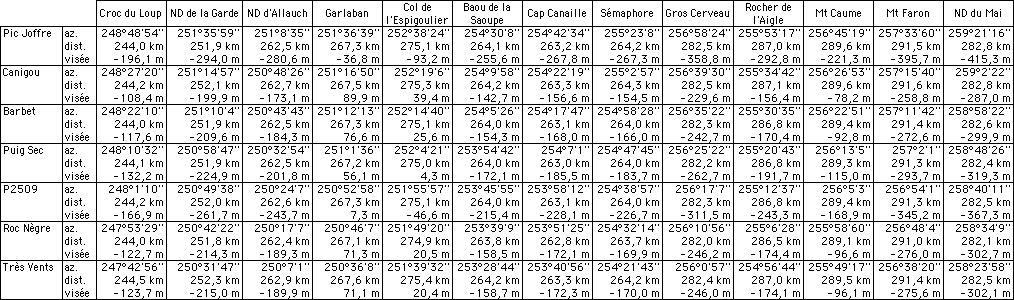
L'image ci-dessus n'est qu'un résumé du fichier Excel téléchargeable, qui comprend tous les calculs intermédiaires.
Dans le fichier complet, les données non calculées (mesurées) figurent en italique :
ainsi que les valeurs de l'ellipsoïde (1/2 grand axe et 1/2 petit axe).
Toutes les autres données sont calculées :
Mes résultats sont différents de ceux de Michel APERIO, car j'ai employé des formules différentes des siennes à certaines étapes.
Je ne retrouve pas non plus la valeur donnée par Yvon GEORGELIN pour la visée directe depuis Notre-Dame de la Garde : il annonce -120 m, alors que mes calculs donnent - 200 m. Toutefois, en prenant pour rayon terrestre 6 365 300 m (valeur employée par GUIGAY dans son article publié en 1972 dans L'astronomie), je trouve bien -120 m...
Si quelqu'un trouve une erreur dans mon raisonnement, qu'il ne se gêne pas pour me la signaler !
détail des calculs :
Soit le triangle :

1) Calcul de CAm le rayon terrestre au niveau du Canigou :
|
|
x = 1/2 grand axe . cos(latA) y = 1/2 petit axe . sin(latA) On applique Pythagore au triangle rectangle : CAm2 = x2 + y2 => CAm |
2) Calcul de b :
b = CAm + AAm
AAm est l'altitude du Canigou => b
3) Calcul de CBm le rayon terrestre au niveau du site d'observation : même chose que pour CAm => CBm
4) Calcul de a : même chose que pour b => a
5) Calcul de CM : même chose que pour CAm ou CBm, en prenant pour latitude la moyenne des latitudes de A et B : latM = (latA + latB) / 2 => CM
Attention : ne pas faire la moyenne des deux rayons terrestres, ça n'a rien à voir !
6) Calcul de l'angle p :
|
|
On travaille dans le triangle sphérique ABP, où P est le pôle nord. cos p = cos m . cos n + sin m . sin n . cos(P) => p |
7) Calcul du côté AB : on résout le triangle quelconque ABC
AB2 = a2 + b2 - 2.a.b.cos(p) => AB
8) Calcul de l'angle A : autre relation dans le triangle quelconque ABC
AB / sin(p) = a / sin(A) => angle A
9) Calcul de la hauteur CF : formule trigonométrique dans le triangle rectangle CAF
sin(A) = côté opposé / hypothénuse = CF / b => hauteur CF
10) Calcul de la visée : la hauteur de la ligne de visée par rapport à l'horizon est tout bêtement CM - CF
CQFD
11) Calcul de la distance : à partir de l'angle p calculé au 6) et du rayon terrestre moyen CM calculé au 5)
|
distance = CM . p |
p en radian ! |
=> distance CQFD
Dans le tableau, ce rayon moyen figure sous l'abrévation Rm.
12) Calcul de l'azimuth : toujours dans le triangle sphérique ABP
cos(m) = cos(n) . cos(p) + sin(n) . sin(p) . cos(A)
=> angle A
azimuth = 360 ° - angle A CQFD
Pour tous les calculs faisant intervenir le rayon terrestre (distance, visée,...), je suggère d'utiliser l'ellipsoïde de Clarke 1880 plutôt que le GRS 80 utilisé par Michel APERIO.
Le GRS 80 est l'ellipsoïde de référence utilisé dans le système géodésique universel WGS 84. Le GRS 80 donne en effet une bonne approximation de la surface moyenne de la Terre aux petites échelles. C'est la raison pour laquelle le WGS 84 a été retenu pour les satellites GPS et le quadrillage kilométrique UTM dont la portée est mondiale.
En revanche, pour des échelles plus grandes, de nombreux pays ont adopté un système géodésique national, basé sur un ellipsoïde plus adapté au pays. En France métropolitaine, l'Institut Géographique National utilise le système RTF 96 basé sur l'ellipsoïde de Clarke 1880 pour déterminer les coordonnées géographiques (latitude / longitude) et le quadrillage kilométrique Lambert.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On constate que l'écart reste très faible, en tout cas inférieur à la précision des positions géographiques que nous avons pu relever, et certainement inférieur à l'écart entre l'ellipsoïde de référence et le géoïde. Si l'utilisation du Clarke 1880 est préférable sur le principe, dans la pratique elle sera nécessaire quand nous aurons relevé la position des différents sites... au 100e de mm !
