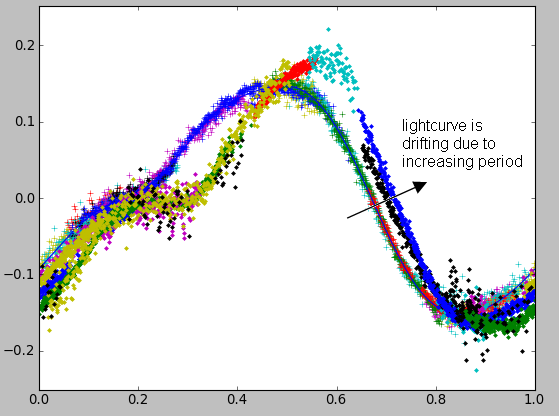
| Back << |
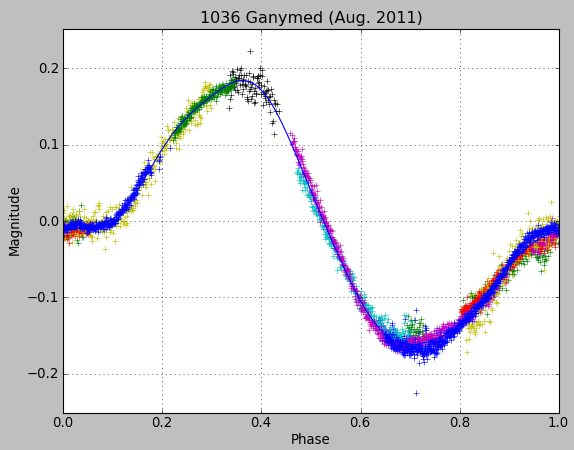
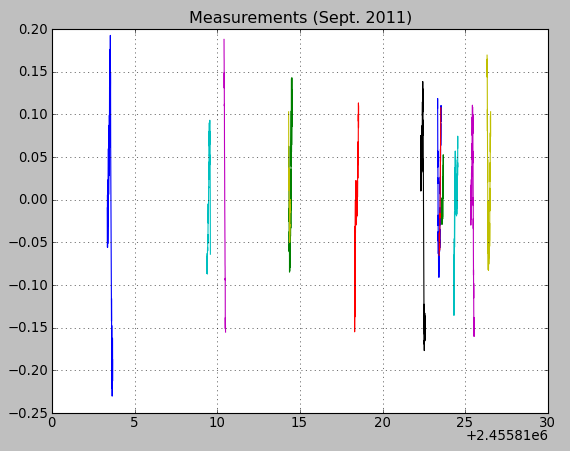
| Measurement in | June-July 2011 | August 2011 | September 2011 |
| from / to | 21 June / 13 July | 09 Aug / 01 Sept | 08 Sept / 01 Oct |
| nb of nights | 13 | 7 | 10 |
| nb of Fourier harmonics | 6 | 6 | 6 |
| period (days) | 0.428976 | 0.429330 | 0.429756 |
| 3-sigma uncertainty (days) | 0.000025 | 0.000035 | 0.000024 |
 |
 |
|
|
|
 |
 |
|
|
|
 |
 |
|
|
|