
Pollution
lumineuse
Par
Michel BONAVITACOLA
A N P C N
et
Jérome CHATAL
INSA Toulouse
Photo : bonavitacola
comète Hale boop vue à 10 km de Toulouse
Passer sur les photos pour avoir les renseignements
 |
Pollution lumineuse
Par Michel BONAVITACOLA A N P C N et Jérome CHATAL INSA Toulouse
Photo : bonavitacola comète Hale boop vue à 10 km de Toulouse |
La pollution lumineuse qu’est ce que c ’est ?
La lumière artificielle des villes part en partie vers le ciel.
Elle est dispersée par les molécules de gaz et les particules de l ’atmosphère.
Il se forme un halo lumineux qui éclaire l ’atmosphère et nous masque ainsi la voûte céleste

Horizon Nord de l ’observatoire du Pic du Midi - Photo Arnauld Pignolo 1995 Club d ’astronomie de Pibrac

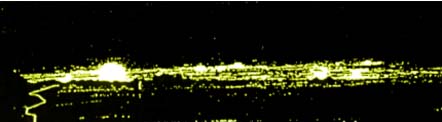
Tucson ( U.S.A ) vue depuis l'Observatoire de Kitt-Peak
 |
 |
Halo lumineux de Blois ( 50000 hab )
Influence de la distance
Halo vu la même nuit de 3 distances différentes. même pellicule ,même appareil et conditions de prise de vue.
A 7 Km, 13 Km et 22 Km.



Cliché de : Christophe Martin-Brisset
|
Comète Hale Bopp à la ville et à la
campagne
|
 |
 |
| Même opérateur et appareil, pellicule, suivi, conditions de prise de vue et météo parfaite . Clichés : Michel Bonavitacola |
Présentation générale du problème
Le phénomène de pollution lumineuse
Description
Le phénomène de pollution lumineuse est très aisé à déceler. En effet, tout le monde a pu remarquer qu'au-dessus des grandes agglomérations se situe un halo lumineux. Il est difficile de discerner un grand nombre d'étoiles lorsqu'on regarde le ciel depuis la place du Capitole, alors que le ciel est d'une qualité bien plus pure en des endroits plus reculés de l'Aveyron, par exemple. Cette dégradation de la qualité du ciel est communément appelée ''pollution lumineuse''.
Tous les instruments optiques utilisés en astronomie (lunette, télescope, œil…) ont des récepteurs particulièrement sensibles, dont les performances sont en général limitées par le bruit photonique du ciel, c'est-à-dire la lumière du fond de ciel naturel sans Lune.
Cette lumière a plusieurs origines : lumière des étoiles non résolues par l'instrument, lumière zodiacale, émissions propres de la haute atmosphère, ainsi que la diffusion de ces lumières par l'atmosphère. L'éclairement correspondant à cette lumière de fond de ciel naturel a comme valeur moyenne 2.10-4 candela m-2, ce qui correspond à une étoile de magnitude 21,6 par seconde carrée sur le ciel (voir plus loin pour la notion de magnitude).
L'illumination directe des instruments par des sources lumineuses artificielles ne constitue pas la source dominante de gêne subie. Elle peut nuire aux observations, soit en éblouissant l'observateur, soit en affectant directement les récepteurs de l'instrument, mais ceci reste un phénomène rare et facilement évité.
La
diffusion par l'atmosphère de la lumière produite à la surface de la Terre (principalement
d'origine artificielle : villes, autoroutes…) a pour effet une augmentation de
la clarté du ciel qui, s'ajoutant à la lumière naturelle du ciel nocturne, augmente
le bruit des photons et diminue ainsi la détectabilité des objets célestes.
Il est bien plus difficile de se protéger de cette gêne-ci.
Le terme
de pollution semble adapté car la gêne provoquée est directement liée aux activités
humaines. Des images saisissantes de la Terre vue de nuit depuis l'espace ont
été prises, et l'on constate que la luminosité des points de la planète sont directement
corrélés avec une activité humaine importante :
villes, axes routiers, industries…
Les photos ci-dessous illustrent parfaitement ce phénomène.
|
|
Il est facile de distinguer sur cette photo les zones de forte population.
Présence de point lumineux en pleine mer du Nord (plate-forme pétrolière…?) |
| L'Europe vue du ciel |
| Sur cette image où les contours de la France ont été ajoutés, les zones les plus actives apparaissent clairement : - grandes villes (Paris, Lyon, Toulouse, Bordeaux…) - axes de communication (vallée du Rhône) - régions touristiques (côte d'Azur, bassin d'Arcachon, côtes du Pays Basque…) |
 |
| La France vue du ciel (couleurs artificielles) |
Gênes provoquées : pauvres astronomes !
La pollution lumineuse gêne tous les amoureux du ciel, ceux qui veulent uniquement contempler les trésors qu'offre naturellement un ciel nocturne. La présence de sources de pollution affecte grandement le nombre d'objets célestes pouvant être observé. Ceci est aisé à comprendre, mais une explication plus rigoureuse est tout de même nécessaire.
La magnitude visuelle des objets ponctuels Depuis l'antiquité les astronomes classent les objets qu'ils distinguent dans le ciel en plusieurs catégories. En effet, tous les objets ne sont pas visibles avec la même facilité. Certains sont très brillants (Lune, Jupiter, Mars, Véga, Sirius…), et d'autres, plus éloignés ou plus petits, ne sont qu'à peine discernables.
Pour avoir un classement rigoureux des objets, la notion de magnitude visuelle a été inventée. Une valeur est attribuée à chaque objet dans le ciel et rend compte de la luminosité de cet objet. Plus la valeur de la magnitude est élevée et plus l'objet considéré est difficile à détecter.
Le système de mesure actuel de magnitude se base sur une formule de mesure relative de la magnitude d'un objet 1 par rapport à une référence 0, à savoir l'étoile Véga dans la constellation de la Lyre :

où
:
M1 et M0 sont les magnitudes visuelles de l'objet et
de la référence
E1 et E0 sont les flux lumineux de l'objet et de la référence, c'est-à-dire le flux reçu par unité de surface du récepteur
Il est évident la valeur d'une magnitude peut être négative. Le passage d'une magnitude à la suivante correspond à un abaissement de luminosité d'un facteur 2,512 : une étoile de magnitude 3 est 2,512 fois plus brillante qu'une étoile de magnitude 4.
Le facteur 2,512 a été retenu car c'est la racine cinquième de 100. Ainsi une étoile de magnitude 1 est cent fois plus brillante qu'une étoile de magnitude 6.
Le tableau ci-dessous donne quelques exemples de magnitudes :
| Nom
| Magnitude |
Nom | Magnitude |
| Sirius
(Grand Chien) | -1.46 | Mercure | -1.9 |
| Véga (Lyre) | 0 | Vénus | -4.4 |
| Bételgeuse (Orion) | 0.2 | Mars | -2.8 |
| Altaïr | 0.77 | Jupiter | -2.6 |
| Aldébaran (Taureau) | 0.85 | Saturne | -0.3 |
| Antarès (Scorpion) | 0.9 | Uranus | 5.6 |
| Epi (Vierge) | 1 | Neptune | 7.7 |
| Pollux (Gémeaux) | 1.14 | Pluton | 13.6 |
| Deneb (Cygne) | 1.25 | ||
| Régulus (Lion) | 1.35 | Lune | -12 |
| Etoile Polaire | 2.15 | Soleil | -27 |
Influence de la pollution lumineuse
Le nombre d'étoiles visibles progresse approximativement d'un facteur 3 à chaque magnitude. Il y a 20 étoiles de première magnitude, 60 étoiles de deuxième magnitude et 180 étoiles de troisième magnitude. On comprend donc l'intérêt de pouvoir discerner des objets de magnitude de plus en plus grande : le nombre d'objets observables croit considérablement !
Il est à noter que les magnitudes des étoiles sont des magnitudes relatives et concernent des objets ponctuels. En effet, les étoiles sont des objets relativement petits en comparaison des distances qui nous séparent d'elles. Les planètes et les objets diffus (telles que les nébuleuses, les galaxies…) possèdent eux une surface apparente dans le ciel. La magnitude moyenne de ces objets peut être calculée, mais elle ne rend pas compte de la finesse des détails que l'on peut observer sur l'objet. On parle pour ces objets (principalement pour les objets diffus) de magnitude surfacique ou brillance surfacique. Cette notion, plus fine, permet de comprendre plus nettement le problème généré par la pollution lumineuse.
Le fond de ciel naturel a une luminosité de 2.10-4 cd m-², ce qui correspond à une magnitude surfacique de 21,6 / sec.arc². Il est évident que tous les objets de magnitude supérieure (donc moins lumineux) sont totalement invisibles, et ce quel que soit le moyen employé.
Il est communément admis que la magnitude limite visible à l'œil nu est à peu près de 6.5 à 7 dans un ciel d'excellente qualité. Si toutefois le fond de ciel nocturne augmente, et même s'il reste nettement en dessous de la luminosité des objets, la magnitude limite de détectabilité va baisser. Les objets de plus forte magnitude ne vont plus être visibles, ou bien l'étendue de l'objet va diminuer, comme l'illustre le graphique suivant:

Impact sur l 'environnement
La luminosité du ciel nocturne ne gêne pas seulement les astronomes. Elle a également des impacts écologiques non négligeables.
L'éclairage artificiel nocturne peut
troubler les rythmes biologiques en déréglant les horloges internes ou certains
processus hormonaux, y compris chez l'homme.
La lumière attire certaines espèces
animales, transformant certaines sources lumineuses en véritables pièges, et effraie
d'autres espèces.
Ces deux effets pervers de la lumière peuvent provoquer un morcellement du continuum biologique, notamment causé par les autoroutes, véritables barrières de lumière. De plus des impacts directs (une espèce ne supporte pas la lumière) et indirects (perte d'une ressource pour un prédateur spécialisé, disparition d'un pollinisateur) sont plus que probables sur les zones fortement éclairées.
Ces effets dévastateurs de la lumière sur l'écosystème sont encore peu étudiés en France, mais il est certain que l'on ne peut réduire le problème de la pollution lumineuse à un problème uniquement d'astronomes et d'amateurs du ciel.
Historique
La lutte contre la pollution et un meilleur aménagement du territoire n'est pas récente. Même si l'ANPCN est une association jeune, elle reflète une réelle prise de conscience des astronomes amateurs de la dégradation des conditions d'observations, due à l'éclairage urbain inadapté pour préserver un ciel sombre et propice au rêve et à l'admiration des merveilles de l'univers.
Voici un bref résumé des actions entreprises et réalisées depuis quelques années dans le domaine de la protection du ciel nocturne -on pourra noter au passage le caractère international des réalisations :
· 1972 : création de l'Association ''Dark Sky Association''. Publication de bulletins, diaporamas grand public
· 1980 : rapport de l'UAI (union astronomique internationale) et de la Commission Internationale de l'éclairage, analysant l'origine des lumières parasites entrant dans les télescopes. La relation avec l'éclairage urbain est sans équivoque.
· 1985 : rapport de l'Académie des Sciences sur la protection des observatoires astronomiques professionnels.
·
De 1988 à 1992 : Espagne : loi votée et textes
législatifs pour protéger l'institut d'astrophysique aux Canaries.
Australie : des règlements locaux sont signés
Etats-Unis : des accords visent à protéger les observatoires
professionnels
· 1992 : sous l'égide de l'UNESCO et organisé par l'UAI, le Comité International des Unions Scientifiques analyse les impacts sur l'astronomie de la ''pollution lumineuse'' dans le cadre des problèmes d'environnement.
·
1993 : signature par les principales associations d'astronomie amateurs
de France d'une charte pour la préservation de l'environnement nocturne.
Celle-ci
s'inscrit dans l'objectif global énoncé dans le droit des générations futures
de la fondation Cousteau
·
1995 : premier congrès national sur la protection de l'environnement
nocturne à Rodez, Aveyron.
Création de "
l'Association Nationale de Protection du Ciel Nocturne".
· 1996 : opération ''Atlas 96'' : mesure de la qualité du ciel de France
· 1997 : rencontres et négociations auprès des ministères et éclairagistes. 140 communes de l'Aveyron ne sont plus subventionnées par le syndicat Intercommunal d'électrification de l'Aveyron si elles décident de poser des lampadaires ''boules''.
· 1998 : premier congrès européen sur la protection de l'environnement nocturne à Paris. deuxième congrès national sur la protection de l'environnement nocturne L'ANPCN (Association Nationale pour la Protection du Ciel Nocturne) a pour but de restaurer et défendre la qualité du ciel nocturne et de sensibiliser les acteurs concernés pour que soient adoptées les mesures appropriées, au plan national et international.
Cette association, dont le siège social est fixé à la Société Astronomique de France (3 rue Beethoven - 75016 Paris) a été fondée dans le cadre de la loi de 1901, par diverses sociétés et associations d'astronomie françaises. Son président est monsieur Martin-Brisset, responsable de ce stage.
Elle a été créé en 1995 au sein de la Société Astronomique de France (S.A.F.), fondée en 1887 par Camille Flammarion, avec le concours de l'Association Française d'Astronomie (A.F.A.), l'Association Nationale Sciences Techniques Jeunesse (A.N.S.T.J.) formant avec la S.A.F. un Comité Inter-Associatif (C.I.A.), et la Société Astronomique de Bourgogne (S.A.B).
Diverses commissions ont été créées pour répondre aux objectifs de l'association. En particuliers, une commission sur la recherche et le développement, au sein de laquelle ce dossier a été effectué.
Le programme THOT
Copyright © M. Bonavitacola. Tous droits reservés

Le programme THOT a été développé par Michel Bonavitacola, chargé de la commission recherche et développement de l'ANPCN. Il a pour but de permettre aux astronomes amateurs de modéliser la pollution lumineuse de leur site. L'objectif est de définir rigoureusement une méthode de calcul d'indice de qualité de site afin de déterminer les sites les plus favorables à l'observation et ainsi pouvoir les protéger.
Les calculs effectués par le programme ont ensuite été vérifiés par des observateurs chevronnés sur des sites sélectionnés. THOT permet (entre autres) à un utilisateur de calculer la pollution lumineuse générée par des villes avoisinantes. Pour cela, la loi de Walker et une méthode de calcul (présentée plus loin) sont utilisées.
L'utilisation de cette fonction est simple : l'utilisateur rentre les coordonnées et la population des villes voisines, ainsi que les coordonnées du lieu où il désire calculer la pollution générée. Le programme lui indique alors l'indice du site considéré, ainsi que la répartition en azimut de la pollution.
Le problème de ce programme vient du caractère manuel de son utilisation : c'est à l'utilisateur de définir les sources de pollution, ainsi que l'endroit où il veut effectuer son calcul. Il est difficile ou rébarbatif de déterminer par exemple un lieu d'observation ''idéal'' situé dans un rayon de 30 km du domicile de l'astronome amateur, le nombre de points de calculs étant trop important.
Nouvel outil d'analyse : les cartes
Le traçage de cartes de pollution lumineuse permet de pallier aux problèmes d'utilisation de la fonction calcul du programme THOT. En effet, il est ici question de calculer pour un grand nombre de points l'indice du lieu, et ensuite de regrouper sur une carte tous les résultats obtenus.
Le but est de réaliser un ensemble de cartes couvrant le territoire national. Il est également en projet de réaliser ces cartes pour d'autres pays, notamment les Etats-Unis. Ces cartes doivent être facilement et rapidement accessibles à n'importe quel astronome amateur qui désire trouver le site le moins pollué et le plus proche.
Génération des cartes
Le problème mathématique :
Modèle existant : la loi de Walker
(voir
rapport de l'académie des sciences - cf bibliographie)
Rapport
de l ’académie des sciences :
Protection des observatoires
astronomiques et géodésiques
J Kovalevsky 1985
un site / une ville Loi expérimental

Afin de calculer la gêne de la lumière produite à la surface de la Terre, il faut modéliser la diffusion par l'atmosphère de ces sources perturbatrices. On ne considère ici que les villes, sources les plus importantes.
La modélisation de la lumière provenant d'une agglomération et diffusée par le ciel est très difficile par suite de la grande quantité de paramètres en jeu : distance et flux lumineux produit par l'agglomération, quantité de gouttelettes d'eau en suspension dans l'air, quantité, dimension et forme des particules. De plus la mesure de qualité d'un site est globale, l'influence de toutes les sources est active, sans pouvoir isoler l'une d'entre elles.
C'est pourquoi, en l'absence de modèle précis et d'expérimentation sur le site, il faut se contenter d'une modélisation simple effectuée sur des sites connus. Une bonne approximation, en considérant des poussières de 1µm , et d'utiliser la diffusion de Raleigh. L'étude de M.F. Walker (Public. Astron. Soc. Of the Pacific, 1977, p.405) donne la relation empirique suivante :
![]()
soit :
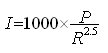 |
où :
I
: rapport d'intensité artificielle de la luminosité du ciel à l'intensité
naturelle
à
45° au-dessus de l'horizon en direction de la ville.
R :
distance en kilomètres de l'agglomération
P
: population de la ville en centaine de milliers d'habitants
Une ville de 100.000 habitants produira donc une augmentation de la brillance du ciel à 45° de hauteur égale à 10% de la clarté naturelle du ciel nocturne si elle est distante de 40 km. A 10 km d'un village de 3.000 habitants, la gêne sera identique.
Hypothèses simplificatrices de la modélisation utilisée
Afin de réduire les paramètres en jeu dans une telle modélisation, il est tout d'abord indispensable de poser certaines hypothèses simplificatrices. Les hypothèses adoptées sont les mêmes que celles du rapport de l'Académie des sciences de 1985, et du programme THOT existant :
- la luminance naturelle du fond de ciel à 45° en direction du zénith est de 2.10-4 candéla/m² , ce qui équivaut à une étoile de magnitude de 21,6 par seconde carrée sur le ciel, - l'air est sec et les conditions d'observations idéales,
- le calcul est effectué pour une élévation de 45° au-dessus de l'horizon dans la direction observateur/ville,
- les seules sources de pollution sont les villes,
- celles-ci ont un rayon constant, et sont donc modélisées par des disques,
- l'accroissement de l'éclat du fond de ciel par rapport à la luminosité du ciel naturel à 45° au-dessus de l'horizon est calculée grâce à la loi de Walker. De plus, on considère qu'une augmentation de 5 % de la luminosité du fond de ciel par rapport à la luminosité naturelle n'est pas détectable. En effet cela correspond à une diminution de la magnitude visible de moins de 0.1 , ce qui n'est pas détectable. On ne calculera donc pas l'augmentation si on sait qu'elle est inférieure à 5 %.
Dans le même ordre d'idée, la loi de Walker a comme domaine de validité l'extérieur des villes. Les augmentations calculées à l'intérieur des villes n'ont aucun sens. Ces deux dernières hypothèses sont très importantes car elles vont directement influencer les calculs présentés plus loin.
Calcul général de la nuisance engendrée
Afin de calculer un indice de qualité de site, il faut définir rigoureusement les pollutions engendrées par les villes avoisinantes suivant leur distance et leur population. La loi empirique de Walker ne suffit pas, nous le verrons plus loin. Il s'agit ici de déterminer l'augmentation de la luminosité du ciel à 45° par rapport au ciel naturel. La méthode présentée ci-dessous a été développée par Michel Bonavitacola.
Nous allons tout d'abord raisonner sur une seule ville, puis nous généraliserons le calcul. L'idée du calcul provient directement de l'observation du halo lumineux généré par une ville, représenté sur la figure ci-dessous :

La ville considérée ici produit une augmentation relative de la luminosité du fond de ciel à 45° égale à celle calculée par la loi de Walker. De plus, on peut étendre cette gêne à un domaine, représenté par l'angle q, qui est en fait l'obstruction de la ville.
En effet, plus la ville est proche, et plus elle apparaît étendue à l'observateur, et la gêne se fera sur une portion plus large du ciel. On peut alors former une fonction de gêne, définie pour toutes les directions depuis le site considéré, et dont la valeur correspond à la gêne des différentes sources :
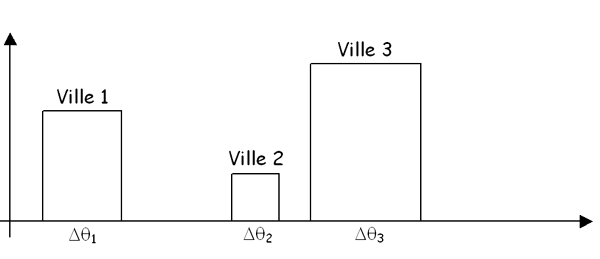
Il ne reste plus qu'à calculer l'intégrale de cette fonction pour obtenir ( à un coefficient 2 p près ) la valeur caractéristique du site. Tout ceci est repris un peu plus rigoureusement ci-dessous ; Suivant la théorie des " indices de qualité " développée par Michel Bonavitacola.
- DL : augmentation de la luminosité du fond de ciel
-DrL : augmentation relative de la luminosité du fond de ciel
- L : luminosité du fond de ciel
- Ln : luminosité du fond de ciel naturel (2.10-4 cd/m², soit 21.6 mag/sec d'arc²)
-Dqi : obstruction de la ville i vue du site
- n : nombre de villes (ou halos) vues depuis le site
L'augmentation relative de la luminosité du fond de ciel est donnée d'une part par la loi de Walker, et d'autre part par la relation :
![]()
d'où :
![]()
La valeur caractéristique du site est définie :

La luminosité du fond de ciel du site à 45° est obtenue en sommant la luminosité naturelle et la luminosité provenant du halo des villes, soit :
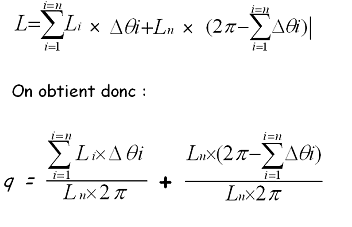

On trouve donc un résultat compréhensible. La somme représente l'intégrale de la fonction présentée ci-dessus, et le '1' est en fait la luminosité naturelle du fond de ciel.
Calcul de l'indice de qualité
L'indice de qualité indique si un site est favorable à l'observation ou non, du point de vue de la pollution lumineuse. Le calcul de cet indice se fait en deux étapes distinctes.
Premièrement, il faut calculer l'augmentation de luminosité à 45° degrés au-dessus de l'horizon. Pour effectuer ce premier calcul, on suit le raisonnement suivant :
- la présence d'une ville implique une augmentation relative de la luminosité du fond de ciel par rapport au ciel naturel. On calcule cet accroissement grâce à la loi de Walker.
- Il faut également déterminer l'obstruction de la ville, c'est-à-dire son rayon apparent. Plus l'obstruction est importante, et plus la gêne provoquée sera grande. Cette obstruction est calculée en radians, puis ramenée en pourcentage.
- La multiplication des deux termes calculés précédemment est la perturbation d'une ville. Cette augmentation est bien sûr adimensionnelle.
- On calcule ainsi la perturbation de chaque source de pollution, puis on ajoute toutes les perturbations. Ensuite, il suffit d'appliquer une grille d'évaluation au résultat obtenu. Cette grille, déterminée grâce aux observateurs chevronnés permet de donner une note (indice de qualité) au site.
Travail à effectuer
Le travail à faire apparaît alors clairement : on se donne un domaine à étudier (France, Midi-Pyrénées, Haute-Garonne…). On maille ce domaine par un maillage régulier et carré. Le pas du maillage dépend de la taille du domaine à étudier. Par exemple, pour la carte générale de la France, le pas utilisé est de 1 km.
Il faut maintenant déterminer pour chaque point du maillage l'indice de qualité du site. Cette détermination suit le raisonnement présenté ci-dessus.
Les sources de pollution (villes) sont répertoriées dans une base de données qui contient le nom, le département, la population ainsi que les coordonnées exactes de la ville. Le programme doit utiliser cette base de données pour placer les sources de pollution sur la carte, effectuer les calculs proprement dits, puis afficher les résultats le plus clairement et le plus complètement possible.
Choix de la modélisation
Les différentes options
Avant de se lancer dans la programmation, il a d'abord fallu déterminer quelle méthode employer, ainsi que le langage de programmation à employer. Après quelques temps de réflexions, deux solutions différentes sont apparues, chacune présentant des avantages et des inconvénients. Après la présentation de ces méthodes, il est précisé ici les critères de choix et la méthode retenue.
Le calcul en fortran
Fortran est un langage de programmation de calcul scientifique et industriel. Il est très puissant dans son domaine d'application, à savoir le calcul.
L'idée d'utilisation de Fortran pour notre problème est la suivante : l'interface avec l'utilisateur est assurée par un programme Visual Basic. L'utilisateur rentre la plage de coordonnées où il désire effectuer son calcul, ainsi que le pas du calcul. Le programme Visual Basic sélectionne les villes qui vont influencer les calculs, en excluant les villes trop éloignées. Il transmet les villes sélectionnées à une routine Fortran, qui calcule les indices de qualité aux points du maillage. L'affichage est assuré par le programme Visual Basic.
Le programme fortran serait composé de trois boucles enchâssées, les deux premières pour parcourir tout le maillage, la dernière pour parcourir toutes les sources potentielles. On teste si la distance est inférieure au rayon d'action de la ville (ce dernier est calculé grâce à une augmentation de 5 %, voir hypothèses simplificatrices, I/2). Si c'est le cas, la ville est une gêne, on lance une routine de traitement de ville. Sinon, on passe à la ville suivante. Une fois ces calculs effectués, on parcourt à nouveaux tout le maillage pour convertir les valeurs 'q' obtenues en indice de qualité.
Ces boucles répétées pour parcourir un maillage totalement régulier et carré fait penser à une gestion matricielle du calcul. C'est pourquoi une autre façon de résoudre le problème est envisageable.
Le calcul par matlab
Matlab (Matrix Laboratory) est un logiciel de calcul matriciel utilisé dans les universités ainsi que par quelques industriels.
L'idée d'utilisation de Matlab est la suivante :
grâce à un fichier de données, on utilise un calcul matriciel (la convolution
discrète) afin de déterminer les valeurs 'q'. Une fonction appliquée à la matrice
des résultats calcule les indices de qualité. Les cartes sont directement générées
par Matlab, enregistrées au format adapté puis lues par un programme Visual Basic.
Les critères de choix
Besoin des utilisateurs
Les utilisateurs ont besoin d'une source de renseignements exploitables pour leurs observations. Il faut une variété suffisante de cartes pour pouvoir satisfaire n'importe quel besoin. L'utilisation la plus commune sera celle d'une personne voulant observer chez lui, ou près de chez lui (moins de 50 km). La question que cette personne se pose est la suivante : quel est, dans un rayon de 50 km, le meilleur site d'observation ? Quelle qualité de ciel peut-on espérer y trouver ?
Il est certain que l'option calcul en Fortran permet une plus grande liberté dans les possibilités de calculs (c'est vraiment ce que l'utilisateur désire). Toutefois, même si une base de données réduit le nombre de cartes possibles, il n'en demeure pas moins que si les bornes et le pas de celles-ci sont bien choisis, ils peuvent suffisamment renseigner l'utilisateur pour que celui-ci ne ressente pas le besoin d'en calculer d'autres. Il serait dans ce cas nécessaire de quadriller la France en plusieurs cartes de pas variables.
Temps de calcul
La rapidité d'utilisation est également ici très importante. L'utilisateurs n'aura pas forcément accès à une capacité de calcul importante, et devra se contenter parfois d'une puissance moyenne. Il est à noter de plus que le nombre de calcul à effectuer est relativement important. Pour chaque point il faut évaluer la gêne de chaque ville voisine. Le nombre de villes gênant un point du maillage dépasse la vingtaine.
On notera au passage que les villes influentes sont bien sûr à déterminer et qu'elles varient d'un point à l'autre : à chaque point il faut tester toutes les villes… Il faut également noter qu'un traitement complet correspond à l'évaluation de la fonction de Walker et au calcul de l'obstruction pour chaque ville. Il faut ensuite sommer les gêne, et convertir le résultat en indice de qualité.
Une évaluation du nombre de calculs à effectuer pour un maillage de 250x250 km avec un pas de 0.5 km est donné ci-dessous :
| Nombre de point du maillage |
500x500 | = 250.000 |
| Nombre de ville à prendre en compte par point : |
x20 | = 5 millions |
| Evaluation de Walker |
x10 | = 50 millions |
| Evaluation de l'obstruction |
x10 | = 500 millions |
On n'a pas pris en compte dans ce calcul la sélection des villes qui est également un calcul relativement important à faire, ni la somme des valeurs caractéristiques, ni la conversion en indice de qualité.
Solution adoptée
Si l'on considère les différents appels à la base de données, à la routine fortran, et le temps d'affichage, le temps mis par un ordinateur moyennement puissant pour afficher une carte peut être important. En revanche, calculer au préalable les cartes, et n'avoir qu'à les afficher est une solution rapide.
C'est pourquoi la solution retenue est celle du calcul des cartes avec un programme Matlab, l'enregistrement de ces cartes dans une banque de données d'images. Celles-ci seront consultées grâce à un programme d'interface Visual Basic.
Explications sur la modélisation
Principe général
L'idée du calcul grâce à Matlab est d'utiliser un produit de convolution (discret) à deux dimensions. La région géographique à traiter est représentée par un maillage régulier, qui forme un ensemble de points que l'on peut stocker sous forme d'une matrice. Les villes sont positionnées sur les points du maillage selon leurs coordonnées, et la valeur attribuée est celle de la population. On obtient donc une matrice qui comporte un grand nombre de valeurs nulles (matrice creuse), les seules valeurs non nulles étant à la place des villes.
Exemple : on désire représenter une zone de 8x8 km, dans laquelle se situe (pour simplifier) trois villes Ville1, Ville2, Ville3, dont on connaît les coordonnées et les populations. La carte est donc modélisée par une matrice 9x9. Les villes sont alignées sur les points du maillage et les valeurs des populations sont reportées dans la matrice. Les points du maillage où il n'y a pas de ville sont mis à zéro. Voir dessins ci-dessous.
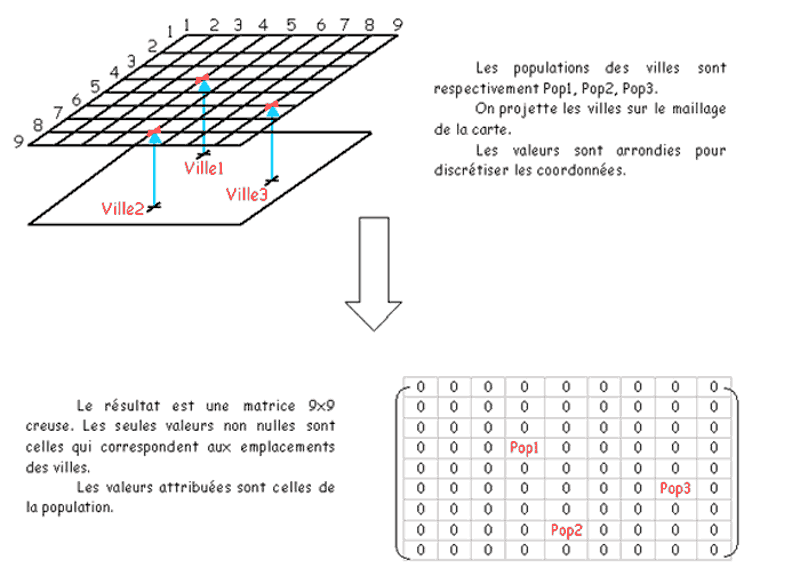
La matrice de la carte étant ainsi formée, on la convolue par un noyau calculé auparavant, qui ''étale'' la pollution en fonction de la valeur de la population de chaque ville. Ce calcul a pour résultat une matrice de la même taille que la matrice-carte originale.
On convertit les valeurs trouvées en indice de qualité, et on affiche enfin le résultat.
La base de données et les coordonnées
La première étape pour réaliser les cartes est d'avoir en données les sources les plus importantes de pollution, c'est-à-dire les villes de France, ainsi que les villes étrangères situées près des frontières. Il faut en particuliers connaître les coordonnées précises de celles-ci ainsi que leur population.
Les données sont stockées dans des fichiers texte lus par le programme Matlab. Le programme crée plusieurs vecteurs (un par champ de donnée). Chaque vecteur a comme longueur le nombre de ville total, et un indice correspond à une seule ville dans tous les vecteurs créés.
La première étape consiste à transformer les coordonnées géodésiques en coordonnées cartésiennes. En effet, la latitude (l) et la longitude (j) sont des angles (voir schéma), et il faut pour le calcul avoir des coordonnées cartésiennes.

On considère que le rayon de la terre est grand par rapport aux distances considérées et on assimile la surface de la Terre (une sphère) à un plan. Les formules de passage du système de coordonnées cylindriques au système de coordonnées cartésiennes donnent :
X = R x cos (l) x ( j- j0 )
Y = R x (l-l 0)
Où :
- R est le rayon terrestre (environ 6350 km)
- l0 est la latitude de l'origine (choisie à 45° nord)
- j0 est la longitude de l'origine (choisie sur le méridien de Greenwich)
On convertit ainsi le vecteur de coordonnées cylindriques en coordonnées cartésiennes. Ce sont ces coordonnées qui vont définir les positions des villes dans la matrice-carte. Il est à noter que les coordonnées utilisées ont comme précision une minute d'angle, c'est-à-dire un soixantième de degré, soit 2.91×10-4 radians. Rapporté en coordonnées cartésiennes, cet angle minimum de précision représente :
DX = 6350 x cos (p/4) x 2.91×10-4 = 1,306 km en moyenne pour les longitudes
DY = 6350 x 2.91×10-4 = 1,847 km pour les latitudes
Ces calculs de précision montrent bien qu'il serait inexact de calculer des valeurs cartésiennes plus précises que le km, qui est la précision adoptée ici. Pour la formation de la base de données en tant que telle, voir l'annexe 1.
N.B : la base de données est limitée !
Il est à noter que la base données utilisée comprend toutes les communes française de plus de 3000 habitants, ainsi que plus de 100 villes étrangères. Ceci est raisonnable pour une première itération de résultat, mais constitue une limite très importante à la validité des résultats. Nous reviendrons plus tard sur ce point, dans la rubrique ''limites et axes de continuation''.
Explications théoriques
Le produit de convolution est une opération mathématique très utilisée dans le domaine de l'imagerie et la théorie du signal. Il est en particuliers utilisé pour modéliser l'action de filtres sur une image originelle. Pour bien expliquer ce dont il est question, prenons l'exemple d'un appareil photo . Cet objet constitue un filtre d'image : en effet l'image originelle (celle que l'on aimerait reproduire à l'identique) n'est pas strictement dupliquée. Si l'on prend en photo une étoile, qui est par définition un point (c'est-à-dire un objet qui n'a pas de surface), la photo obtenue montrera une tâche blanche, dont le caractère flou dépend directement de la qualité de l'appareil et du film utilisé.
En théorie du signal, on modélise l'action de l'appareil photo par un produit de convolution. Ce produit peut être interprété comme une multiplication ''régularisante'' de l'image originelle. Le schéma ci-dessous montre le phénomène en dimension un.

La façon dont le signal devient flou est définit grâce au noyau de convolution. C'est lui qui représente le filtre (dans l'exemple : l'appareil photo lui-même).
On parle de convolution discrète quand le signal d'entrée n'est pas connu en tout point, mais en seulement en un ensemble de points dénombrables. En langage mathématique, l'espace de départ est inclus dans N et non plus dans R. Il est nécessaire d'utiliser un produit en deux dimensions, une pour les latitudes, et une pour les longitudes.
Formalisons ces considérations. Soit une image T de taille n x m. On convole cette image par un filtre U de taille p x q (p et q sont supposés pairs).
Le résultat V est donné par la formule :

![]()
Le résultat obtenu ici est de taille ( m+p ) x ( n+q ). Il faudra donc tronquer les valeurs extrêmes pour obtenir une matrice résultat de même taille que la matrice initiale. De plus, par besoin de symétrie, le noyau devra être centré en zéro. Ces points sont abordés plus bas.
Application au problème
L'idée est de calculer un noyau de convolution d'une ville témoin. Ceci fait, on convole la matrice-carte trouvée par ce noyau. La population de la ville sera alors transformée, ''étalée'', par l'opération de convolution.
L'application au problème est immédiate du moment la fonction ''gêne'' est linéaire par rapport à la population. Il est très important de noter que c'est cette linéarité qui a assurer l'exactitude des résultats obtenus. Attardons-nous donc sur ce point.
Pour cela, il va d'abord falloir démontrer que la convolution par un noyau quelconque est une application linéaire, et que cette méthode ne peut donc rendre compte que d'une pollution linéairement liée à la population.
Soient donc deux matrices X et Y de taille n x m et un réel l = 0. On calcule les pollutions générées grâce à un noyau de convolution U, de taille p.
Il est facile de vérifier les propriétés de linéarité de la convolution par U :

La
convolution par un noyau de pollution témoin est donc une application linéaire
par rapport aux valeurs de X, c'est-à-dire les valeurs de population.
Si la fonction pollution à calculer n'est quant à elle pas linéaire, les résultats
trouvés seront faux.
Cette fonction est calculée à partir du principe. La gêne provoquée par une ville dépend donc de l'augmentation relative de luminosité par rapport au fond de ciel naturel, et de l'obstruction de la ville.
La loi de Walker calcule l'augmentation relative de luminosité de fond de ciel par rapport au ciel naturel. Cette augmentation (DrL) ne dépend que de deux facteurs, la population de la ville-source et la distance du point par rapport à la ville. La dépendance de DrL par rapport à la population P est linéaire.
Toutefois l'autre facteur, l'obstruction, demande plus d'attention.
Gestion de l'obstruction : division en catégories
Définition de l'obstruction
L'obstruction est l'angle apparent sous lequel on perçoit une ville. Il est évident que pour une ville de taille donnée on la percevra beaucoup plus grande si on se trouve plus proche d'elle.
Si on se trouve à une distance D d'une ville de rayon R, l'angle apparent q est :

Plus l'obstruction est grande et plus la ville sera gênante.
La fonction 'rayon' : nouvelle modélisation
On voit donc qu'il nous faut connaître le rayon des villes pour pouvoir calculer l'obstruction. Pourtant, ce renseignement ne fait pas partie des données dont on dispose dans les bases de données brutes. Il va donc falloir estimer le rayon de chaque ville. Les hypothèses utilisées sont que les villes ont un rayon fixé et égal dans toutes les directions. Il est de plus supposé que le rayon ne dépend que de la population.
Afin d'estimer au mieux la fonction qui calcule le rayon
suivant la population de la ville, le rayon moyen des villes est mesuré sur
une carte IGN, puis les villes sont tracées sur un repère. En abscisse les populations
sont reportées, et on positionne les rayons en ordonnée. Au vue des points trouvés,
il semble pertinent de modéliser la fonction rayon de la forme : ![]() ,
les points suivant une courbe similaire à ceux d'une fonction racine carré.
,
les points suivant une courbe similaire à ceux d'une fonction racine carré.
Les deux coefficients
a et b, réels, sont à déterminer.
Ceci est un problème d'optimisation,
il faut minimiser la somme des erreurs : ![]() ,où
,où![]() sont
les points mesurés.
sont
les points mesurés.
L'étude est volontairement restreinte
à des plages de valeurs cohérentes avec les mesures, à savoir aÎ[1
; 10] et bÎ[0.1 ; 1].
La précision souhaitée ne peut être trop exigeante, c'est pourquoi elle est
choisie de 0,1 pour a et de 5×10-2 pour b.
On trouve les valeurs numériques a = 3,6 et b = 0,35.
Représentée sur un graphique avec les points expérimentaux, voici la fonction ainsi calculée :

La division en catégories
Un grand problème se pose alors : l'obstruction ne dépend pas linéairement du rayon (fonction arc tangente) et d'ailleurs le rayon n'est pas une fonction linéaire de la population, comme nous venons à peine de le voir.
Pour résoudre ce problème, une division en catégories de villes est nécessaire. On découpe en fait l'ensemble des villes en groupes de villes dont le rayon est à peu près égal. Au lieu d'avoir une fonction rayon comme celle présentée ci-dessus, on va en fait utiliser une fonction escalier proche de celle-ci , avec une hauteur de pallier de 0,2 km.
Voici une représentation de cette nouvelle fonction celle implémentée dans le code :

On va alors résoudre le problème par bloc, c'est-à-dire qu'on va tout d'abord considérer qu'il n'y a que des villes de catégorie 1, calculer la pollution générée, puis considérer uniquement les villes de deuxième catégorie, et ainsi de suite. On sommera les influences à la fin, juste avant le passage aux indices.
Pour
chaque catégorie, on va créer un noyau de convolution différent, qui saura traiter
l'obstruction comme une fonction linéaire par rapport à la population.
En
effet, pour les populations au sein d'une même catégorie, un seul rayon sera utilisé,
et il sera employé pour former le noyau correspondant à la catégorie.
La
fonction obstruction n'aura donc plus comme variable la population, et les résultats
obtenus seront donc corrects.
Génération du noyau de convolution
Prise en compte des paramètres
Pour générer le noyau de convolution, il faut prendre en compte l'augmentation de luminosité grâce à la loi de Walker et gérer l'obstruction.
On se souvient des hypothèses
faites au I/2) : à l'intérieur des villes, la loi de Walker n'a pas de sens. Comme
elle tend vers l'infini quand R tend vers zéro
(on se rapproche du centre
de la ville), il faut la saturer. On bloque donc la valeur résultat à 500 lorsqu'on
se situe dans la ville.
Si l'on représente la fonction de Walker pour une ville témoin de 100.000 habitants, on obtient :

Les valeurs n'ont été ici représentées que jusqu'à 10 pour plus de clarté. La ville se situe aux coordonnées (50 ; 50). Les valeurs calculées correspondent à l'augmentation de luminosité du fond de ciel provoquée par une ville de 100.000 hab. dans sa zone d'influence. Par exemple, au point (20 ; 50), qui se situe à 30 km de la ville, la surface représentée est à la hauteur de l'augmentation en ce lieu.
De même, pour l'obstruction, on calcule pour les points environnants la largeur angulaire apparente de la ville. La valeur est saturées à 2p à l'intérieur de la ville. Si l'on représente l'obstruction d'une ville de 50.000 habitants, on obtient :
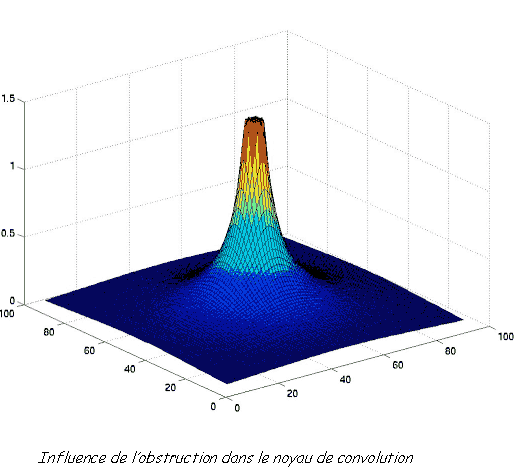
On a volontairement représenté les valeurs du noyau précédant jusqu'à p/2, ceci pour plus de clarté dans la représentation. La ville est bien évidemment située au point [50 ; 50] du plan.
L'influence réelle de la ville sur la région est donc la multiplication des deux noyaux précédemment trouvés. Il est à noter en particulier que cette méthode calcul permet assez facilement de prendre en compte d'éventuels nouveaux paramètres plus fins de gêne.
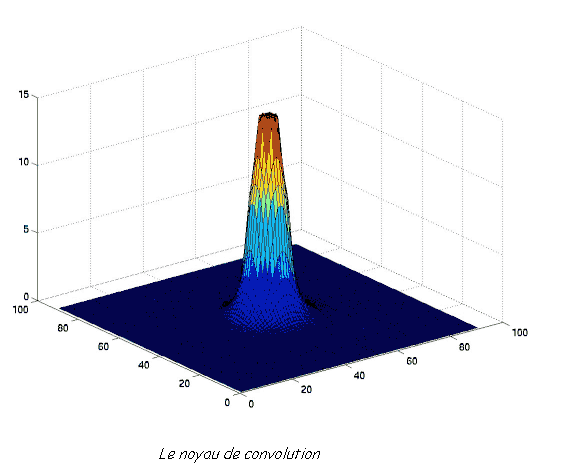
Le noyau utilisé dans les calculs pour une ville de cette catégorie peut donc être représenté sous la même forme que précédemment. Les valeurs sont saturées à 15 pour plus de lisibilité.
Il est important de comprendre que les valeurs représentées sont en fait des valeurs d'augmentation globale de luminosité par rapport à un ciel naturel. Par exemple, une valeur de 4 correspond à une augmentation de 400 % par rapport à un ciel non pollué.
Adaptation automatique de la taille du noyau
Il est nécessaire de ne pas utiliser la même taille pour toutes les catégories de villes. En effet, une ville de 7.000 habitants n'a pas une étendue de pollution comme une ville de 200.000 habitants. C'est pourquoi il faut avant tout déterminer la distance de gêne d'une ville. Pour ce faire, on inverse la loi de Walker, en prenant une gêne de 5 %. On trouve la loi suivante, qui a comme résultat la distance de gêne Dg d'une ville d'une population P :
![]()
Il est alors inutile de calculer l'influence de la ville donnée à une distance supérieure à celle calculée ci-dessus, car elle ne sera pas détectable. Pour optimiser la rapidité des calculs, on fait donc varier la taille du noyau de convolution à chaque changement de catégorie. Pratiquement, si la distance de gêne d'une catégorie est Dg, alors la taille T du noyau correspondant sera :
![]()
Le passage aux indices
Une fois obtenues les valeurs caractéristiques de pollution d'un lieu, il faut pouvoir traduire la valeur trouvée en indice de qualité, c'est-à-dire exprimer si un site est correct ou bien mauvais. L'indice de qualité est un chiffre compris entre 0 (exécrable) et 10 (très bon) déterminé par des astronomes expérimentés, qui se basent sur des critères établis, d'une part l'observation à l'œil nu des objet étendus, et d'autre part la détermination de la magnitude limite de vision.
Cette conversion est un point particulièrement délicat du présent problème. En effet, l'ensemble théorique du calcul des valeurs caractéristiques est démontré à partir de considérations scientifiques et physiques (loi de Walker, calculs physiques homogènes et cohérents). Il peut bien entendu être remis en cause dans ses fondements, mais constitue un tout cohérent, qui est appréhendé de façon identique par les différents interlocuteurs scientifiques. Une fois les idées et principes acceptés, les résultats ne peuvent pas être remis en cause.
Ceci n'est pas le cas du passage aux indices de qualité. Ce n'est plus en effet un problème de démonstration et de mesures physiques, mais une estimation subjective de chaque observateur, chacun jugeant suivant ses expériences et ses connaissances. C'est pourquoi il a été demandé à des observateurs chevronnés de déterminer une échelle de conversion entre les valeurs caractéristiques de pollution et les indices de qualité.
Grâce à messieurs Mosser, Rieugnié, Hoffer et Bonavitacola, une échelle de conversion est aujourd'hui disponible. La méthode utilisée pour la réaliser est cohérente. Répartie sur des sites de qualités différentes, et utilisant un protocole spécifique, la notation de chaque site a permis de déterminer une première grille de conversion. Toutefois d'autres campagnes d'observations sont nécessaires afin de valider les premières conclusions, et des mesures plus rigoureuses (scientifiquement parlant), avec notamment l'emploi de caméra CCD.
Présentation de l'algorithme
Le programme se compose d'une fonction principale qui a comme argument les quatre limites de la carte à tracer : latitude inférieure, latitude supérieure, longitude inférieure, longitude supérieure, ainsi que le pas et le nom de base pour les fichiers en édition.
Une fois ces coordonnées limites entrées, le programme fait appel à la base de données de villes complète, et sélectionne les villes qui vont avoir une influence sur la carte à tracer, en utilisant la fonction de distance de gêne décrite ci-dessus.
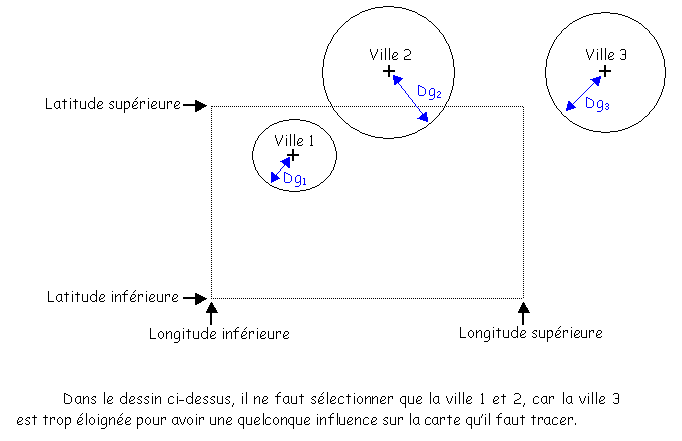
Une fois les villes correctement sélectionnées, il faut à présent les classer par catégories. Ce classement se fait tout naturellement par la valeur de leur rayon. Il y a 37 catégories : une de chaque valeur de rayon de 0,2 à 7,2 par pas de 0,2 et une dernière qui regroupe toutes les plus grande villes (supérieures à 700.000 habitants).
Grâce aux coordonnées limites et au pas donnés, on définit la taille de la matrice résultat. Puis, pour chaque catégorie, une matrice d'influence est calculée. Cette matrice, de la même taille que la matrice résultat, représente l'influence de toutes les villes de la catégorie en cours.
On crée donc tout d'abord le noyau de convolution adéquat, puis la matrice d'influence de la catégorie, vierge. On place les villes comme il est décrit dans la partie III/1), et on effectue la convolution par le noyau précédemment calculé. Il suffit d'ajouter la matrice influence ainsi trouvée à la matrice résultat générale.
On se retrouve donc à la fin de ce traitement avec une grande matrice résultat. Cette matrice donne les valeurs caractéristiques de pollution des points du maillage. Il faut à présent convertir ces valeurs en indice de qualité de site, en utilisant la table de conversion déterminée par les observations des astronomes chevronnés.
Enfin, plusieurs modes d'affichage et de sauvegarde d'image sont utilisés, pour obtenir une large palette de possibilité d'utilisations.
Voici l'organigramme de ce programme :

Résultats obtenus
Les cas tests
Afin de vérifier la validité des calculs effectués, plusieurs cas tests ont été réalisés. Tout d'abord des cas tests simples, en plaçant trois villes au hasard et quatre villes en carré (cas symétrique). Plusieurs points sont récupérés directement sur les résultats du programme, et comparés à des calculs effectués à la main. Une étude d'erreur est présentée. Enfin, on teste les résultats sur la région Midi-Pyrénées.
Cas tests simples
Cas test
Trois villes imaginaires Ville1, Ville2 et Villes3 sont disposées sur une carte de 100 km de côté. Les populations et les coordonnées sont données ci-après :
| Nom |
Population | X |
Y |
|
Ville 1 | 300000 |
10 | 10 |
| Ville 2 |
200000 | 80 |
40 |
|
Ville 3 | 100000 |
20 | 90 |
Voici la carte obtenue :

Cinq mesures sont effectuées, avec d'une part les résultats du programme, et d'autre part le résultat du calcul fait indépendamment.
| Point
de contrôle | 1 |
2 | 3 |
4 | 5 |
| Abscisse |
20 | 20 |
70 | 30 |
80 |
| Ordonnée |
10 | 80 |
40 | 30 |
90 |
| q programme | 1.4492 |
0.3504 |
0.8703 |
0.0439 |
0.0037 |
| q manuel | 1.4495 |
0.3504 |
0.8703 |
0.0445 |
0.0044 |
| Dq | 3×10-4 |
<10-4 | <10-4 |
6×10-4 | 7×10-4 |
| Indice programme |
5 | 6 |
6 | 9 |
10 |
| Indice manuel | 5 |
6 | 6 |
9 | 10 |
| D indice | 0 |
0 | 0 |
0 | 0 |
Les résultats obtenus sont satisfaisants. En effet l'erreur absolue la plus large est inférieure à 10-3, ce qui est 20 fois plus faible que le niveau de détermination de l'indice le plus bas (et donc le plus sensible), qui est de 2×10-2.
On constate également qu'il n'y a aucune erreur sur les indices de qualité.
Cas test
Quatre villes imaginaires Ville1, Ville2, Villes3 et Ville4 sont à présent disposées sur une carte de 10 km de côté, chacune occupant un angle du carré ainsi formé. Les populations et les coordonnées de ces villes sont données ci-après :
| Nom |
Population | X |
Y |
|
Ville 1 | 10000 |
0 | 0 |
| Ville 2 |
10000 | 0 |
10 |
| Ville
3 | 10000 |
10 | 0 |
| Ville 4 |
10000 | 10 |
10 |
Voici la carte obtenue :

Cinq mesures sont effectuées, avec d'une part les résultats du programme, et d'autre part le résultat du calcul fait indépendamment.
| Point
de contrôle | 1 |
2 | 3 |
4 | 5 |
| Abscisse
(km) | 1.5 |
4 | 2 |
5 | 5 |
| Ordonnée
(km) | 1.5 |
1 | 2 |
3 | 5 |
| q
programme | 3.2001 |
0.4600 | 1.2908 |
0.2616 | 0.2131 |
| q
manuel | 3.2001 |
0.4600 | 1.2908 |
0.2616 | 0.2131 |
| Dq | <10-4 |
<10-4 | <10-4 |
<10-4 | <10-4 |
| Indice
programme | 4 |
6 | 5 |
6 | 6 |
| Indice
manuel | 4 |
6 | 5 |
6 | 6 |
| D
indice | 0 |
0 | 0 |
0 | 0 |
Ici aussi les résultats sont très satisfaisants, avec des erreurs de valeurs caractéristiques inférieures à 10-3 et aucune erreur d'indice.
La région Midi-Pyrénées
Après les cas test 1 et 2
purement numériques, un autre cas test est calculé pour confronter le nouveau
processus aux mesures effectuées sur le terrain.
Il s'agit de la région Midi-Pyrénées.
On procède de la même manière que précédemment, en utilisant ici des observations
directes sur site pour vérifier les calculs de Matlab.
Tout d'abord voici la carte de la région considérée, éditée par le programme :

Ensuite, les points mesurés sont confrontés aux prévisions :
| Villes |
Mesures sur place |
Calcul progamme |
| St Giniès Bellevue |
3 | 3 |
| Pibrac |
5 | 5 |
| St Caprais |
7 | 8 |
| St Cricq |
9 | 8 |
| Marut |
9 | 9 |
Il
apparaît ici des différences de résultats entre les observations directes et les
résultats du calcul.
En ce qui concerne St Caprais, on peut penser que le problème vient de la base
de données, qui doit être insuffisamment fournie pour rendre compte de
cette région.
Par contre, pour St Cricq, la différence n'est pas
expliquée.
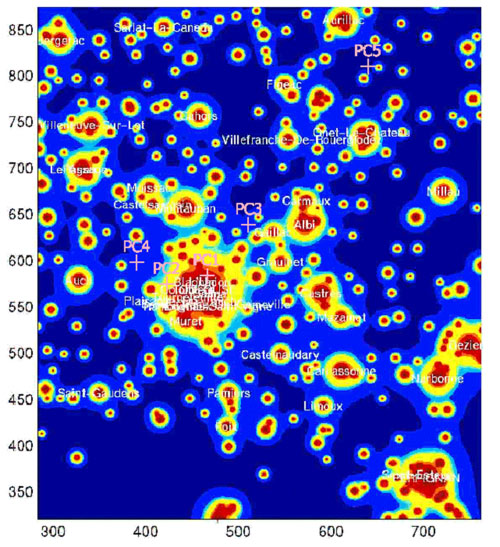
Les cartes éditées
Copyright © M. Bonavitacola. Tous droits reservés
Une fois la méthode conçue et testée, il reste à générer les cartes proprement dites. Outre une carte de France générale éditée pour symboliser les résultats obtenus, il est absolument nécessaire d'éditer les cartes qui vont servir aux utilisateurs sur le terrain. A cette fin, il faut découper le territoire français en zones. Le découpage suit relativement scrupuleusement celui du mini atlas routier Michelin 2001. Pour chaque zone considérée, quatre types de cartes sont éditées, afin d'obtenir un large éventails de possibilités d'utilisation : une carte aux contours remplis vierge de noms, une carte aux contours remplis également avec les noms des principales localités, une autre série avec un maximum de villes nommées (la carte restant tout de même lisible) . La dernière série de cartes est vierge de noms, et reprend les données de la première série, avec une modification pratique : au lieu d'avoir des contours remplis, ils sont uniquement délimités. Ceci permet aux utilisateurs d'imprimer plus facilement cette carte et de partir sur le terrain vérifier la qualité du ciel prévue. Il y a donc 28 zones différentes, et quatre types de carte par zone, ce qui fait 112 cartes éditées. Elles sont produites au format jpg, afin d'avoir une taille réduite et d'être facilement transportable (format le plus courant pour les images)
 |
Carte de France
des indices de site de la Pollution lumineuse
|
| Itération 1 : Images calculées par : Michel Bonavitacola et Jérôme Chaptal |

Voici le découpage utilisé :

Limites et axes de recherche
La base de données
Il apparaît que la première contrainte à l'exactitude des résultats est la taille limitée de la base de données. En effet, la base actuelle contient toutes villes françaises de plus de 3.000 habitants, ainsi que quelques autres communes de moins de 3.000 habitants. Même si cette base est raisonnable, il n'en demeure pas moins qu'elle ne représente que 72,6 % de la population française. Les perturbations calculées sont donc plus optimistes qu'il ne le faudrait.
De même, les chiffres des populations utilisés datent de 1995. Il est donc probable que les populations ont augmenté et donc que la qualité du ciel est plus médiocre qu'elle n'est affichée. Afin de résoudre ces problèmes, il faudrait tout d'abord actualiser la base de données de populations françaises. L'INSEE propose un produit adaptée à cette mise à jour.
De même, l'IGN propose un produit où les coordonnées de toutes les communes de France sont répertoriées. Ceci constitue un investissement probablement profitable, même si la base de l'IGN semble chère (plus de 2.000 francs !).
La fonction azimut
Dans les cartes éditées, les calculs ne tiennent pas comptent de l'azimut de la source de pollution. En terme physique, ceci ne constitue pas une gêne, le ciel étant de toute façon isotrope. Cependant, pour les astronomes la situation est différente. En effet toutes les directions ne sont pas équivalentes et une source de pollution sera bien plus gênante si elle se situe au sud que si elle est au nord.
Toutes les étoiles du ciel ont un mouvement apparent de rotation autour de l'étoile polaire. C'est pourquoi certaines étoiles sont dénommées étoiles circum polaire - autour de la polaire. On peut alors distinguer plusieurs types d'étoiles : celles qui sont visibles durant toute l'année (les circum polaires) et d'autres qui ne sont visibles qu'à certaines périodes de l'année. Il est évident que plus on s'éloigne de l'étoile polaire et plus le temps durant lequel on peut voir une étoile est court. D'un autre côté, plus on est éloigné de l'étoile polaire, et plus le nombre d'objets que l'on peut observer est grand. C'est pourquoi il est beaucoup plus profitable pour un astronome de pouvoir observer en direction du nord qu'en direction du sud.
Il est donc souhaitable de pouvoir intégrer cette notion dans le calcul des indices de qualité du ciel. La solution à trouver est de déterminer une fonction azimut qui pondèrerait le calcul déjà réalisé. Cependant trouver une telle fonction n'est pas facile, et demande un travail de recherche conséquent. Une fonction azimut a été trouvée, mais un problème de conversion (voir plus loin) rend difficile de l'utiliser.
Une fois cette fonction déterminée, la structure du programme reste ouverte pour l'intégrer le plus facilement possible. Au lieu d'avoir deux facteurs dans la formation du noyau de convolution (la fonction de Walker et l'obstruction), il suffirait de rajouter la fonction azimut, le reste des calculs demeurant identique jusqu'au passage en indice. En effet il se poserait ici un problème de taille : l'échelle des valeurs élaborée ne tient pas compte de ces pondérations.
Donc pour utiliser une fonction azimut, il faudrait un nouveau travail sur le terrain afin de qualibrer le modèle, étape longue et laborieuse. Une ébauche de réflexion sur une fonction azimut possible est fournie en annexe
Les problèmes de mémoire
Lors de l'exécution du programme, il est apparu certains problèmes de mémoire, dus à la taille des matrices à calculer. En effet, pour la carte de France en particulier, la taille de la matrice résultat est de l'ordre de 1100 x 1200, ce qui représente un tableau à plus d'un million de composantes. Convoler cette matrice avec le noyau correspondant aux plus grandes villes (soit un noyau de taille supérieure à 100 x 100) est une opération très coûteuse !
Il y a plusieurs solutions pour résoudre ce problème : soit augmenter la puissance de calculateur, soit trouver une nouvelle méthode pour traiter les plus grandes villes. Augmenter la puissance du calculateur pourrait être réalisé en se procurant Matlab sous PC. Quant à trouver une autre méthode de calcul, ceci reste possible. En fait, une tentative pour résoudre autrement le problème a été faite. Plutôt que de convoler le noyau avec la matrice résultat, on multiplie le noyau par la population de la ville et on ajoute la gêne au bon endroit dans la matrice résultat.
Toutefois cette méthode n'a pas réussit à résoudre le problème, la machine se déclarant hors de capacité pour des valeurs à peu près comparables à la méthode de convolution. Il est à noter que ce problème de mémoire est à l'origine du pas des 15 premières cartes, car Paris a une influence sur toutes ces cartes, et nécessite un noyau de convolution d'une grande taille. Cette limite posera un problème certains dans l'établissement futur des cartes des Etats-Unis, par exemple, car le pays contient beaucoup de grandes villes.

Voie Lactée : Photo de E.Mallard
ITERATION 2 - Stage ANPCN / INSEA - Stagiaire : Nicolas Prestat
Voici
l'échelle ainsi déterminée (ce code de couleur est utilisé pour les cartes) :
| > 30 | 3 mauvais | Centre ville | |
| {2 ; 30} | 4 médiocre | Banlieue | |
| {1 ; 2} | 5 passable | Grande banlieue | |
| {0,15 ; 0,2} | 6 moyen | Périphérie | |
| {0,1 ; 0,15} | 7 correct | Campagne | |
| {0,02 ; 0,1} | 8 bien | Isolé | |
| 0,02 | >9 très bien | Très isolé |
Il est à noter que d'autres échelles de qualité
ont été établies par des astronomes chevronnés
(sans correspondance cependant
avec les valeurs caractéristiques, spécificité de l'échelle ci-dessus).
 Itération 2 : Images calculées par : Michel Bonavitacola et Nicolas Prestat |
|
| Recalage du nouveau modèle Le recalage de l ’ancienmodèle
a été établi sur | |
 |
 |
 |
Effet de masquage : Massif des Bauges - Vallée de la Tarentaise |
 |
Modèle d’atmosphère
standard
modèle de la diffusion de Rayleigh


Modèle d ’atmosphère standard

ITERATION 3 - Cartes, dernier modèle
Voir le Chapitre " La Voie Lactée à l'œil "dans le numéro 6 du Nez en l'air ( www.astrosurf.com/nezenlair )

Campagne SOS 2003
 |
Echelle
de Bortle Magnitudes limites Objets Messier visibles à l ’œil nu Voie
Lactée |
 |
Conclusions

Dossier
écosystèmes :
Florient Lamiot
Législation
/ aspects juridique :
Armelle Guignier .
Rapport de stage Parc régionaux
/ Parcs nationaux/ Réserves naturelles Paysages
Les réserves naturelles ont aussi pour mission de protéger les paysages le jour mais aussi la nuit
Les
espèces animales et végétales qui peuplent les réserves
naturelles doivent être protégées le jour comme la nuit
La vie se déroule aussi la nuit
Communiquer et négocier auprès des responsables des parcs et élus
 La
pollution lumineuse concerne tout le monde !!!
La
pollution lumineuse concerne tout le monde !!!
Des
solutions techniques et peu coûteuses existent
La législation existe mais doit encore évoluer.
Les
astronomes amateurs et professionnels doivent s'impliquer activement sur le terrain
pour faire évoluer les choses
Apprendre
à communiquer et à négocier Envisager des formations
Des associations existent et travaillent dans ce sens
Projet d'éclairer la neige la nuit avec de puissants projecteurs : il faut lutter contre cela !!!






|
La nature est un livre sublime que nous ne
devons pas nous lasser de lire,
|
 |
il est écrit pour toutes les âmes. Nul livre humain ne peut lui être comparé !!!! Vivre la contemplation du beau, dans la poèsie de la nature et de l'art, dans la recherche du vrai et du bien. Quelle vie pourrait être superieure à celle-là. Je n'en ai pour ma part jamais abandonné d'autre
Camille Flammarion |
| Eclipse du 11 août 1999 : Cliché de Michel Bonavitacola |
ADRESSES
En France
ANPCN : 3 rue de Beethoven 75016 Paris ( Siége de la SAF )htpp://www.astrosurf.com/anpcn
Liste Noire : htpp://groupe yaohh.com/groupe/cielnoir
Radio Astro : htpp://www.obs-nancay.fr
Impact sur la faune et la flore, Direction Environnement-Energie-Déchets, Conseil Régional du Nord-Pas de Calais : deed@cr-npdc.fr
CARL, CERA, Planétarium du Forum des Sciences Villeneuve d'Ascq
Dans le Monde
International Dark-Sky Associatio ( IDA ) http://www.darsky.org/
New England Light Pollution Advisory Groupe ( NELPAG )
Officina Tecnica para la Protecion de la Calidad del cielo ( OTPC )
Instituto de Astrofisica de Canarias ( IAC )
Bibliographie
· Rapport du premier et deuxième Congrès National sur la Protection du Ciel Nocturne (Rodez, Aveyron, 3/4 octobre 1998)
· Impacts écologiques de l'éclairage nocturne, article de Mr Floriant Lamiot, extrait du précédant rapport.
· Rapport du groupe de travail sur la protection des observatoires astronomiques et géophysiques, Académie des Sciences - Comité des Etudes et Rapports (Grasse, 18 novembre 1984)
· Atlas routier de France 2001, 1 :1 000 000, Michelin Editions des Voyages