The Tsiolkovsky formula

Konstantin Tsiolkovsky (1857-1935) was a mathematics teacher in Kaluga (about 150 km in the south-west of Moscow). He was the first scientist in the world to take an interest in spaceflight and established the basics of rocketry as early as the end of the nineteenth century. In 1896, he began the writing of his manuscript « Exploration of the Universe with Reaction Machines » which was published in 1903 (one century already!). In this work, he describes a spacecraft propelled by a rocket engine (a jet engine able to work in vacuum) fueled by liquid oxygen and liquid hydrogen in the front of which the pilot is installed in a pressurised cabin with an oxygen reserve, and estabishes for the first time the laws of motion for a changing-mass body with an equation which has since become known as the Tsiolkovsky formula.

In a second edition published in 1914, he brought significant improvements to his project by adding a gyroscopic control and a stabilisation system by jet deviation. He also proposed the use of new propellants as hydrocarbons and even imagined an atomic rocket engine working with radium desintegration. He was also the first to propose multistage rockets as the solution to fly to Earth orbit.

Introduction

The demonstration of the Tsiolkovsky formula or final velocity formula is quite simple without taking into account neither gravitational field nor atmospheric drag. This fundamental equation is the basis of current spacecraft engineering.

The conservation of momentum (quantity of motion) over the time interval yields the equality between momentum of exhausted gases and increase of rocket momentum :

[1]

where d_e is the gas flow expressed in kg/s, v_e the velocity of exhausted gases expressed in m/s, M the rocket mass over the time interval dt expressed in kg, and dv the velocity increase over the interval dt.

Equation [1] can be written following Newton's second law of motion :

[2]

where the term is the thrust F expressed in Newtons and the rocket acceleration expressed in m/s².

Making the assumption that the gas flow d_e is constant over the total combustion time T_c, the mass M can be written as follows :

[3]

The final mass is then :

[4]

Reporting [3] in [1] yields :

[5]

which has to be integrated between 0 et T_c to get the total velocity increase ΔV :

[6]

Introducing the variable in equation [6] yields :

[7]

which gives the final velocity of a rocket in vacuum without gravity or Tsiolkovsky formula :

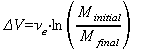[8]

In practice, a jet engine is caracterized by its specific impulse Isp which is the time expressed in seconds during which the engine provides a thrust of a kilogram with a kilogram of propellant. In other words, it is the time during which the engine provides an acceleration equal to Earth's gravity with one kilogram of propellant. Longer is this time, more efficient is the engine.

The specific impulse is linked to the exhaust velocity by the following equation :

[9]

where g₀ is the gravity acceleration at Earth's surface (~9,81 m/s²).

The Tsiolkovsky formula can be rewritten then :

[10]

This equation assumes that the specific impulse is constant in time, which is an approximation since a rocket engine is more efficient in vacuum than at atmospheric pressure. It doesn't take into account neither gravity field (gravity losses) nor atmospheric resistance (drag losses).

The difference between starting mass and ending mass is the propellant (fuel and oxidizer) mass used. The current technology limits this difference : the mass of a non reusable structure (mass without payload or propellant, or dry mass) is at least 6% of the total mass in the case of the couple RP-LOX (kerosene-liquid oxygen) and at least 9% of the total mass in the case of the couple LH2-LOX (liquid hydrogen-liquid oxygen) due to hydrogen low density ; for information, the dry mass of the Concorde represents about 50% of the total mass at take-off. The ratio dry mass / total mass is called the structure index.

The following table gives the specific impulse in vacuum for the main technologies (fuel-oxidizer) of the best current rocket engines :

1. 10% loss at atmospheric pressure

2. 20% loss at atmospheric pressure

Table 1 – Current engine performance

A velocity of 7800 m/s is required to fly to Earth orbit at an altitude of 200 km. In practice, the effective velocity increase ΔV needs to be about 1700 m/s higher than the putting-into-orbit velocity to compensate gravity and drag losses, so the launcher capacity must be at least 9500 m/s. The launch trajectory is calculated to minimize the total losses and results from a trade-off : a vertical launch minimizes drag losses but maximizes gravity losses while a horizontal launch minimizes gravity losses but maximizes drag losses.

Single stage launchers

Considering a ΔV of 9500 m/s and table 1, we get the following maximum index of structure for a single stage vehicule (SSTO for Single Stage To Orbit ) from equation [10] for the couples RP-LOX et LH2-LOX :

Table 2 – Maximum index of structure for a SSTO

The calculated mass ratios represent the structure mass (payload included) relative to the total mass. The use of kerosene and liquid oxygen prevents from launching with a SSTO as the current technology requires a structure index greater than 6% with such propellants. The use of liquid hydrogen and liquid oxygen is possible but the payload mass is limited to 2% of the total mass since an index of structure greater than 9% is required with these propellants.

As for designing a reusable SSTO, this is another story : it seems to me that all the corresponding projects were abandoned. The solution to this difficult issue is certainly the development of a hydrogen rocket engine capable of using the atmospheric oxygen in the first part of the flight to get a better global specific impulse.

The difficulties made by a launch with a single stage vehicle are so great that a multistage launcher is still required nowadays. For information, the first Sputnik was launched with a two-stage rocket.

Dual stage launchers

The formula of velocity increase in the case of a two-stage launcher can be easily written from equation [10] :

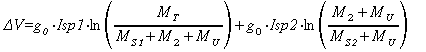[11]

with :

[12]

where :

• M_T, total mass, payload included

• M_U, payload mass

• M₂, total mass of second stage

• M₁, total mass of first stage

• M_S2, dry mass of second stage

• M_S1, dry mass of first stage

• Isp2, specific impulse of second stage

• Isp1, specific impulse of first stage

The effective velocity increases are estimated with equation [11] for the three assemblies :

• 1^st stage RP+LOX et 2^nd stage RP+LOX (ex : Zenith)

• 1^st stage LH2+LOX et 2^nd stage LH2+LOX

• 1^st stage RP+LOX et 2^nd stage LH2+LOX (ex : Saturn V Skylab)

The analysis is run considering the two parameters :

• payload mass relative to lift-off mass : M_U/M_T

• second stage mass relative to propulsive assembly mass : M₂/(M₁+M₂)

with the following indexes of structure :

• 1^st stage RP+LOX : 6%

• 2^nd stage RP+LOX : 6%

• 1^st stage LH2+LOX : 12%

• 2^nd stage LH2+LOX : 9%

Firstly, we notice that in all cases the optimum combination is a second stage four to five times lighter than the first stage : thus for the two-stage Saturn V used to launch Skylab in 1973, the first stage mass was 2286 t (t for metric ton) while the second stage mass was 491 t.

Secondly, a two-stage RP+LOX launcher can fly to Low Earth Orbit (LEO) with a payload equal to about 3% of its total mass : thus the Zenith launcher has a LEO capacity of 13.7 t which represents 3% of the total lift-off mass.

Thirdly, a launcher with a first stage RP+LOX and a second stage LH2+LOX can put into LEO a payload equal to about 5% of its total mass : thus the two-stage Saturn V of 2916 t could put into LEO a payload of 116 t which represents 4% of the total lift-off mass. The difference is explained by the lower efficiency of the engines designed 35 years ago (Isp of 300 s for the first stage and of 425 s for the second stage) relatively to the performances indicated table 1 for current rocket engines : in this particular case the calculation of ΔV shows that such a launcher can put into LEO a payload equal to about 4% of its total mass (QED!).

Lastly, a two-stage LH2+LOX launcher could put into LEO a payload equal to about 6% of its total mass. The gain relative to the previous case is quite low considering the difficulties encountered in implementing hydrogen : it seems to me that this architecture has never been used.

Of course, all these calculations are the product of « Sunday engineering », nevertheless the orders of magnitude are verified in practice and the findings are consistent.

01 January 2004

English edition on 30 May 2004

Bibliography :

[R1] L'astronautique soviétique, Christian Lardier, Armand Colin, 1992

[R2] Guide des lanceurs spatiaux, Sergueï Grichkov, Tessier & Ashpool, 1992

[R3] Le Grand Atlas Universalis de L'Espace, 1989