Documentation technique de Calaphot
[Calaphot]
Algorithme global
Dans cette section ne sont décrites que les fonctions propres aux calculs de photométrie. Toutes les fonctions graphiques ou relatives à l'interface humain sont ignorées.Principe de base des calculs
Calaphot est un script dédié à des calculs de photométrie différentielle effectués sur une série d'image. Chaque image est considérée individuellement. Et donc dans une image donnée, on mesure le flux d'un astéroïde et les flux d'étoiles dites de référence qui ont été sélectionnées au préalable. Les flux des étoiles de référence sont aggrégés en un flux unique représentant ainsi une super-étoile. La magnitude catalogue des étoiles de référence étant connue au préalable, celui de la super-étoile s'en déduit par une formule simple. De ces trois données (flux de l'astéroïde, flux de la super-étoile, magnitude de la super-étoile), on en déduit immédiatement la magnitude de l'astéroïde par appilcation directe de la formule de Pogson.Etoiles de référence.
Les étoiles de référence sont des étoiles qui à priori ont une photométrie considérée comme stable pour la durée totale couverte par les images à étudier. Mais il se peut que cette présomption s'avère fausse, soit qu'une ou plusieurs étoiles soient en fait variables, ou que durant la durée des poses, l'atmosphère absorbe différemment les radiations de ces étoiles en fonction de leur classe spectrale (effet du à la variation de la masse d'air). Pour mettre en évidence cette possible variabilité des étoiles de référence, on effectue un calcul similaire à celui effectué pour l'astéroïde, mais en utilisant une pseudo-super-étoile. Pour une étoile de référence donnée, sa pseudo-super-étoile sera formé à partir de toutes les étoiles de référence autres qu'elle-même.- Cas où une seule étoile de référence est sélectionnée : dans ce cas, la comparaison avec une pseudo-super-étoile n'a pas de sens, et ce calcul n'est pas fait. La possible variabilité de cette étoile de référence ne peut pas être mise en évidence.
- Cas où deux étoiles de référence sont sélectionnées : chaque étoile de référence est comparée à son alter-égo. On obtient alors deux courbes de variabilité symétriques, sans qu'il soit possible de dire si l'une est meilleure que l'autre.
Constante des magnitudes.
La constante des magnitudes est la magnitude d'un astre fictif dont le flux serait 1 ADU pour un temps de pose de 1s. Ce calcul est fait pour chaque image à partir du flux de l'étoile de référence et permet de caractériser la transparence du ciel. Sur une nuit très claire, le profil de la constante des magnitudes dessine une courbe en cloche, témoin de la variation de la masse d'air que doit traverser les photons issus des étoiles de référence. Par nuit brumeuse, on voir aussi nettement se dessiner les instants de passage des bancs de nuages élevés (baisse de cette valeur). Ce calcul est juste informatif, mais il permet de repérer rapidement dans une séquence les périodes où les mesures sont les meilleures.Séquencement des opérations.
- Saisie d'une certain nombre de paramètres nécessaires aux calculs :
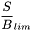 : rapport signal sur bruit limite.
: rapport signal sur bruit limite.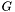 : gain inverse de la caméra (en électron/ADU).
: gain inverse de la caméra (en électron/ADU).- paramètres spécifiques à la photométrie d'ouverture.
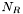 : bruit de lecture de la caméra (en électrons).
: bruit de lecture de la caméra (en électrons).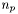 : facteur de division des pixels.
: facteur de division des pixels.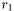 : rayon exprimé en FWHM du disque entourant l'astre (nécessaire à la mesure du flux de l'astre).
: rayon exprimé en FWHM du disque entourant l'astre (nécessaire à la mesure du flux de l'astre).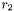 : rayon interne exprimé en FWHM de la couronne entourant l'astre (nécessaire à la mesure du flux de fond de ciel).
: rayon interne exprimé en FWHM de la couronne entourant l'astre (nécessaire à la mesure du flux de fond de ciel).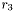 : rayon externe exprimé en FWHM de la couronne entourant l'astre (nécessaire à la mesure du flux de fond de ciel).
: rayon externe exprimé en FWHM de la couronne entourant l'astre (nécessaire à la mesure du flux de fond de ciel).
- Sélection de l'astéroïde à étudier.
- Sélection des
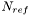 étoiles de référence, et entrée de leur magnitude catalogue
étoiles de référence, et entrée de leur magnitude catalogue 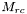 .
. - Calcul de la magnitude de la super-étoile
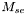 à partir des
à partir des 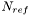 valeurs
valeurs 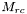 . Celle-ci est donc une constante pour toutes les images qui vont être traitées
. Celle-ci est donc une constante pour toutes les images qui vont être traitées - Boucle pour toutes les images.
- Modélisation de tous les astres par une nappe gaussienne de façon à déterminer précisément le centroïde ainsi que d'autres paramètres utilisés en photométrie d'ouverture.
- Mesure du flux de l' astéroïde
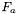 .
. - Mesure du flux de chacune des étoiles de référence
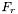 .
. - Calcul du flux de la super-étoile
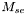 .
. - Calcul de l' incertitude sur la magnitude de la super-étoile.
- Calcul de la magnitude de l'astéroïde
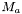 .
. - Calcul de l' incertitude sur la magnitude de l'astéroïde
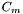 .
. - A titre de vérification, calcul des magnitudes des étoiles de référence (à partir de leur pseudo-super-étoile).
- A titre de vérification, calcul des incertitudes sur les étoiles de référence (à partir de leur pseudo-super-étoile).
- Filtrage à partir des rapports signal sur bruit..
- Calcul de la constante des magnitudes.
- Fin boucle pour toutes les images.
- Filtrage à partir de la constante des magnitudes
Détail des calculs.
Mesure des flux des astres.
- Photometrie d'ouverture : Toutes les étoiles de référence ont préalablement été modélisés. On dispose pour chacune de ces étoiles des paramètres de l'ellipse qui l'englobe (
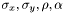 ).
).- Ellipse moyenne : on détermine tout d'abord une ellipse moyenne de paramètres (
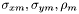 ) par
) par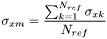
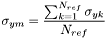
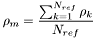 où
où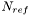 est le nombre d'étoile de référence.
est le nombre d'étoile de référence. et
et 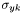 sont les écarts-types sur les axes principaux de l'ellipse de l'étoile de référence
sont les écarts-types sur les axes principaux de l'ellipse de l'étoile de référence 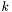 .
.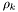 est le facteur d'allongement de l'étoile de référence
est le facteur d'allongement de l'étoile de référence 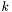 .
.
- Disque interne : puis on détermine une fenêtre d'ouverture elliptique d'axes
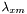 et
et 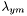 et de facteur d'allongement
et de facteur d'allongement 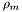 centrée sur l'étoile.
centrée sur l'étoile.

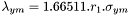 où
où
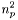 sous-pixels,
sous-pixels, 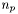 étant le facteur de division entré par l'utilisateur. Ainsi chaque sous-pixel se voit attribuer un niveau de gris égal à celui du pixel divisé par
étant le facteur de division entré par l'utilisateur. Ainsi chaque sous-pixel se voit attribuer un niveau de gris égal à celui du pixel divisé par 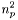 .Finalement, on détermine sur l'image l'ensemble des sous-pixels qui sont englobés par l'ellipse et on somme les niveaux de gris de ces sous-pixels dans
.Finalement, on détermine sur l'image l'ensemble des sous-pixels qui sont englobés par l'ellipse et on somme les niveaux de gris de ces sous-pixels dans 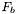 . On récupère aussi le nombre décimal de pixels
. On récupère aussi le nombre décimal de pixels 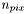 inclus dans la fenêtre.
inclus dans la fenêtre. - Couronne externe : on procède de même pour déterminer 2 cercles définissant une couronne dans laquelle sera mesuré le niveau de gris du fond de ciel. Les rayons de ces 2 cercles sont donnés par
- cercle interne :
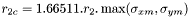
- cercle externe :
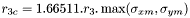
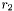 est le rayon interne exprimé en FWHM de la couronne qui entoure l'astre à mesurer. Il a été spécifié par l'utilisateur.
est le rayon interne exprimé en FWHM de la couronne qui entoure l'astre à mesurer. Il a été spécifié par l'utilisateur.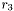 est le rayon externe exprimé en FWHM de la couronne qui entoure l'astre à mesurer. Il a été spécifié par l'utilisateur.
est le rayon externe exprimé en FWHM de la couronne qui entoure l'astre à mesurer. Il a été spécifié par l'utilisateur.
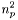 sous-pixels. A partir de tous les sous-pixels compris dans la couronne, on mesure alors le niveau de gris moyen
sous-pixels. A partir de tous les sous-pixels compris dans la couronne, on mesure alors le niveau de gris moyen 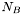 du fond de ciel par pixel, ainsi que le nombre de pixels (décimal) correspondant à la surface de la couronne
du fond de ciel par pixel, ainsi que le nombre de pixels (décimal) correspondant à la surface de la couronne  .
. - cercle interne :
- Le flux
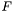 de l'astre considéré est déterminé par
de l'astre considéré est déterminé par 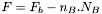
- Ellipse moyenne : on détermine tout d'abord une ellipse moyenne de paramètres (
- Photométrie par modélisation : L'astre est tout d'abord modélisée par une nappe gaussienne. Le flux
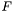 est défini par le volume compris entre la nappe modélisant le profil de l'étoile et le plan du fond de ciel.
est défini par le volume compris entre la nappe modélisant le profil de l'étoile et le plan du fond de ciel.
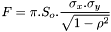 où
où : niveau de gris maximum au niveau du centroïde
: niveau de gris maximum au niveau du centroïde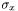 et
et 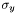 : écart-types suivant les axes principaux de l'ellipse
: écart-types suivant les axes principaux de l'ellipse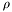 : facteur d'allongement de l'ellipse (
: facteur d'allongement de l'ellipse (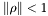 )
)
- Photométrie par SExtractor : SExtractor inclue un module de photométrie qui est documenté dans le chapitre 9.4 du SExtractor user's manual. Calaphot utilise ce module avec les options suivantes :
- DETECT_TYPE CCD
- MAG_ZEROPOINT 0.0
- GAIN mis à la valeur entrée par l'utilisateur.
- BACK_SIZE 32
- BACK_FILTERSIZE 3
- BACKPHOTO_TYPE GLOBAL
- MAG_AUTO
- MAGERR_AUTO
- FLUX_AUTO
- FLUXERR_AUTO
Calcul du flux de la super-étoile.
Le flux de la super-étoile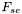 est déterminé en sommant les flux
est déterminé en sommant les flux 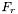 des
des 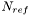 étoiles de référence.
étoiles de référence.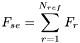
Calcul du flux de la pseudo-super-étoile.
Le flux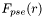 de la pseudo-super-étoile
de la pseudo-super-étoile 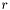 (qui sert à vérifier le comportement de l'étoile de référence
(qui sert à vérifier le comportement de l'étoile de référence 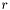 ) est déterminé en sommant les flux
) est déterminé en sommant les flux 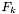 des
des 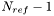 étoiles de référence autres que l'étoile de référence
étoiles de référence autres que l'étoile de référence 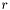 ).
).
Calcul des magnitudes.
- Magnitude de l'astéroïde : le calcul de la magnitude utilise la formule de Pogson, la référence étant fournies par la magnitude et le flux de la super-étoile
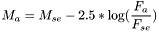 où
où
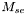 est la magnitude de la super-étoile
est la magnitude de la super-étoile
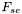 est le flux mesuré de la super-étoile
est le flux mesuré de la super-étoile
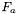 est le flux mesuré de l'astéroïde
est le flux mesuré de l'astéroïde
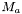 est la magnitude de l'astéroïde
est la magnitude de l'astéroïde
- Constante des magnitudes : la constante des magnitudes est la magnitude d'un astre fictif dont le flux intégré sur une unité de temps (ici la seconde) correspond à 1 ADU au dessus du fond de ciel. Son calcul se fait à partir des flux et magnitudes de la super-étoile.
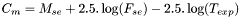 où :
où :
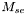 est la magnitude de la super-étoile
est la magnitude de la super-étoile
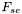 est le flux mesuré de la super-étoile
est le flux mesuré de la super-étoile
 est le temps de pose (exprimé en seconde) de l'image considéré
est le temps de pose (exprimé en seconde) de l'image considéré
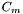 est la constante des magnitudes.
est la constante des magnitudes.
- Magnitude de la super-étoile :
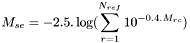 où
où
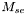 est la magnitude de la super-étoile
est la magnitude de la super-étoile
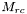 est la magnitude catalogue de l'étoile de référence no r
est la magnitude catalogue de l'étoile de référence no r
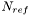 est le nombre d'étoile de référence
est le nombre d'étoile de référence
Calcul d'incertitude sur les magnitudes
- Photométrie d'ouverture : la formule générale (dite équation générale des CCD) est tirée de [1]. Elle donne le rapport signal à bruit
 :
:
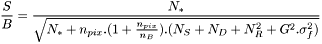 où
où
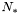 est le nombre total de photons correspondant à l'étoile.
est le nombre total de photons correspondant à l'étoile.
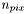 est le nombre de pixels de l'étoile.
est le nombre de pixels de l'étoile.
 est le nombre total de pixels utilisés pour calculer le fond de ciel moyen.
est le nombre total de pixels utilisés pour calculer le fond de ciel moyen.
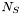 est le nombre de photons par pixel correspondant au fond de ciel.
est le nombre de photons par pixel correspondant au fond de ciel.
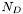 est le nombre d'électrons par pixel du courant d'obscurité.
est le nombre d'électrons par pixel du courant d'obscurité.
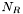 est le nombre total d'électrons par pixel générés par le bruit de lecture du CCD.
est le nombre total d'électrons par pixel générés par le bruit de lecture du CCD.
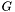 est le gain de la caméra CCD (exprimé en electron / ADU.)
est le gain de la caméra CCD (exprimé en electron / ADU.)
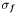 est un facteur constant valant approximativement 0.289.
est un facteur constant valant approximativement 0.289.
- Note:
- Les mots photon et électrons sont des synonymes dans les expressions ci-dessus, on devrait normalement parler de photo-electron, notion qui intégrerait le rendement quantique du CCD.
Pour des observations avec des caméra CCD classiques, dont le gain est assez élevé, on peut négliger les 2 termes . La formule ci-dessus est exprimée en photons (ou électrons). Or, les mesures sur les images s'effectuant en ADU, cette formule devient alors (en reprenant les notations ci-dessus )
. La formule ci-dessus est exprimée en photons (ou électrons). Or, les mesures sur les images s'effectuant en ADU, cette formule devient alors (en reprenant les notations ci-dessus )
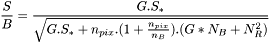 où :
où :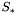 est le nombre d'ADU correspondant à l'étoile
est le nombre d'ADU correspondant à l'étoile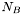 est le nombre d'ADU par pixel du fond de ciel
est le nombre d'ADU par pixel du fond de ciel
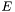 sur la mesure de la magnitude est donnée par
sur la mesure de la magnitude est donnée par 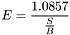 .
.
- Photometrie par modelisation . L'incertitude sur le flux est directement issue du calcul des paramètres de la modélisation de l'astre. (voir Modélisation d'une étoile par une nappe gaussienne. )
- Photometrie par SExtractor . voir le paragraphe sur la mesure des flux par SExtractor.
Calcul des incertitudes totales.
- Pour la super-étoile, l'incertitude
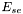 est calculée à partir des incertitudes
est calculée à partir des incertitudes 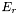 et des magnitudes mesurées
et des magnitudes mesurées 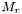 de chacune des
de chacune des 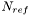 étoiles de référence :
étoiles de référence :
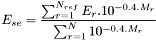
- Pour l' astéroïde, l'incertitude totale
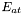 est la somme de son incertitude propre
est la somme de son incertitude propre 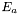 et de celle de la super-étoile
et de celle de la super-étoile 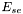
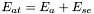
- Cas particulier des étoiles de référence : pour une étoile de référence
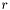 , on calcule l'incertitude de la pseudo-super_étoile
, on calcule l'incertitude de la pseudo-super_étoile 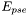 , puis l'incertitude globale de l'étoile de référence
, puis l'incertitude globale de l'étoile de référence 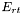 à l'aide des formules (
à l'aide des formules (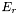 désignant l'incertitude propre de l'étoile de référence)
désignant l'incertitude propre de l'étoile de référence)
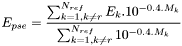 .
.
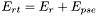 .
.
où les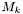 designent les magnitude mesurées des étoiles de référence autres que l'étoile
designent les magnitude mesurées des étoiles de référence autres que l'étoile 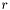 .
.
Modélisation d'une étoile par une nappe gaussienne.
La modélisation permet de trouver une fonction analytique qui soit la plus proche au sens des moindres carrés de la fonction de niveaux de gris d'un astre. On peut trouver plus de détails dans les conférences de Peter B. Stetson. Dans le cas de la nappe gaussienne, la fonction de modélisation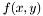 est donnée par
est donnée par 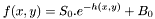 où
où 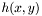 vaut
vaut 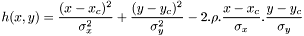 Il faut noter que l'équation
Il faut noter que l'équation 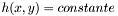 est l'équation au centre d'une ellipse, dont les axes sont proportionnels aux valeurs
est l'équation au centre d'une ellipse, dont les axes sont proportionnels aux valeurs 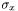 et
et 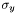 . Pour les notations :
. Pour les notations : est le niveau de gris maximum au niveau du centroïde.
est le niveau de gris maximum au niveau du centroïde.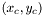 sont coordonnées du centroïde.
sont coordonnées du centroïde.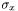 et
et 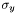 sont écart-types suivant les axes principaux de l'ellipse.
sont écart-types suivant les axes principaux de l'ellipse.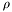 est le facteur d'allongement de l'ellipse (
est le facteur d'allongement de l'ellipse (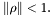 )
)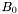 est le niveau de gris du fond de ciel.
est le niveau de gris du fond de ciel.
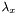 le FWHM suivant un des axes de l'ellipse,
le FWHM suivant un des axes de l'ellipse, 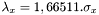
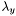 le FWHM suivant l'axe perpendiculaire au précédent,
le FWHM suivant l'axe perpendiculaire au précédent, 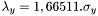
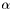 l'angle entre les axes principaux de l'ellipse et les axes de l'image.
l'angle entre les axes principaux de l'ellipse et les axes de l'image.
- si
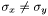 , on a
, on a 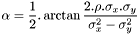 .
.
- dans le cas contraire, l'ellipse est un cercle, et
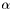 est indéterminé.
est indéterminé.
- si
Filtrage des images
Certaines images de mauvaise qualité, ou dont les résultats semblent aberrants doivent être écartées du rapport final.Filtrage à partir des rapports signal sur bruit.
Ce filtrage vise à éliminer les images douteuses. Sont qualifiées de douteuses les images dont au moins un astre a un rapport signal à bruit inférieur à la limite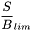 définie par l'utilisateur. Ce filtrage est fait au fur et à mesure des calculs.
définie par l'utilisateur. Ce filtrage est fait au fur et à mesure des calculs. Filtrage à partir de la constante des magnitudes
La constante des magnitudes étant calculée directement à partir du flux de la super-étoile, son évolution dans le temps est sensée être lente et ne suivre que les variations de la masse d'air. On peut donc s'appuyer sur sa valeur pour tenter de détecter rapidement les images qui semblent aberrantes pour des raisons diverses (passage nuageux, disfonctionnement de la caméra, dérive brutale brutale du télescope, etc...)L'algorithme est le suivant : pour une image donné, on calcule la moyenne
 et l'écart-type
et l'écart-type 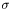 de la constante des magnitudes pour les 5 images précédentes et les 5 images suivantes. Si la constante des magnitude de l'image donnée est dans l'intervalle
de la constante des magnitudes pour les 5 images précédentes et les 5 images suivantes. Si la constante des magnitude de l'image donnée est dans l'intervalle ![$ \displaystyle [m-3.\sigma, m+3.\sigma] $](form_98.png) , l'image est conservée. Elle est rejetée dans le cas contraire, et ne participera plus au calcul de la moyenne et écart-type pour les images suivantes. S'il y a moins de 5 images avant ou après l'image donnée, on ne prend que celle qui existent (éternel problème des bords).
, l'image est conservée. Elle est rejetée dans le cas contraire, et ne participera plus au calcul de la moyenne et écart-type pour les images suivantes. S'il y a moins de 5 images avant ou après l'image donnée, on ne prend que celle qui existent (éternel problème des bords).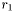 est le rayon exprimé en FWHM du disque elliptique qui entoure l'astre à mesurer. Il a été spécifié par l'utilisateur.
est le rayon exprimé en FWHM du disque elliptique qui entoure l'astre à mesurer. Il a été spécifié par l'utilisateur.  1.5.6
1.5.6