EINSTEIN TO HUBBLE TELESCOPE
Hubble an experience to disprove relativity

INDEX

Section 1) Einstein's theory where it comes from?
Section 2) Focal displacement with light speed change
A) If Einstein was wrong the effect on space telescope
B) Wave theory and focal displacement in reflection
Section 3) Hubble proves our theory
A) It was not a structural defect.
B) Astronomers comments for near objects
C) Astronomers comments for far objects
D) Press release as published
Section 4) Theory light propagation
Section 5) Michelson Morley experiment
Section 6) Details of calculations

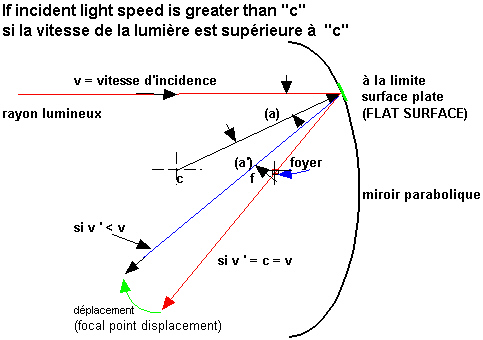
Section 2) Focal displacement with light speed change

A) If Einstein was wrong ?

Let say that Einstein was wrong and the speed of fossil light from 100 of millions light years away is not at 300 000 but faster say at 312 000 km / sec. What would happened if this light falls on a spherical mirror of a space telescope. First from Michelson's experience we know that the reflected light speed would be at 300 000 km / sec. That would be catastrophic. The image would focus away from its design value because of the change in the speed of light before and after it impacted the mirror. You can verify, that the focal point will move, from this independent source, the second answer given in :
Ref.#7-a) (Reflection angle is not always the same )

Above is the diagram # 2 showing the light reflecting on a parabolic mirror at a lower speed than the incident light.
Based on the wave propagation theory we obtain that the reflected ray angle (a') is no longer the same as the incident ray. When we apply the theory to a spherical mirror the focal distance increases going away from the mirror. This results in a blurred image for a fixed focus system. In Section 2) - B just below, we give you the explanations based on Huygens' theory for wave front

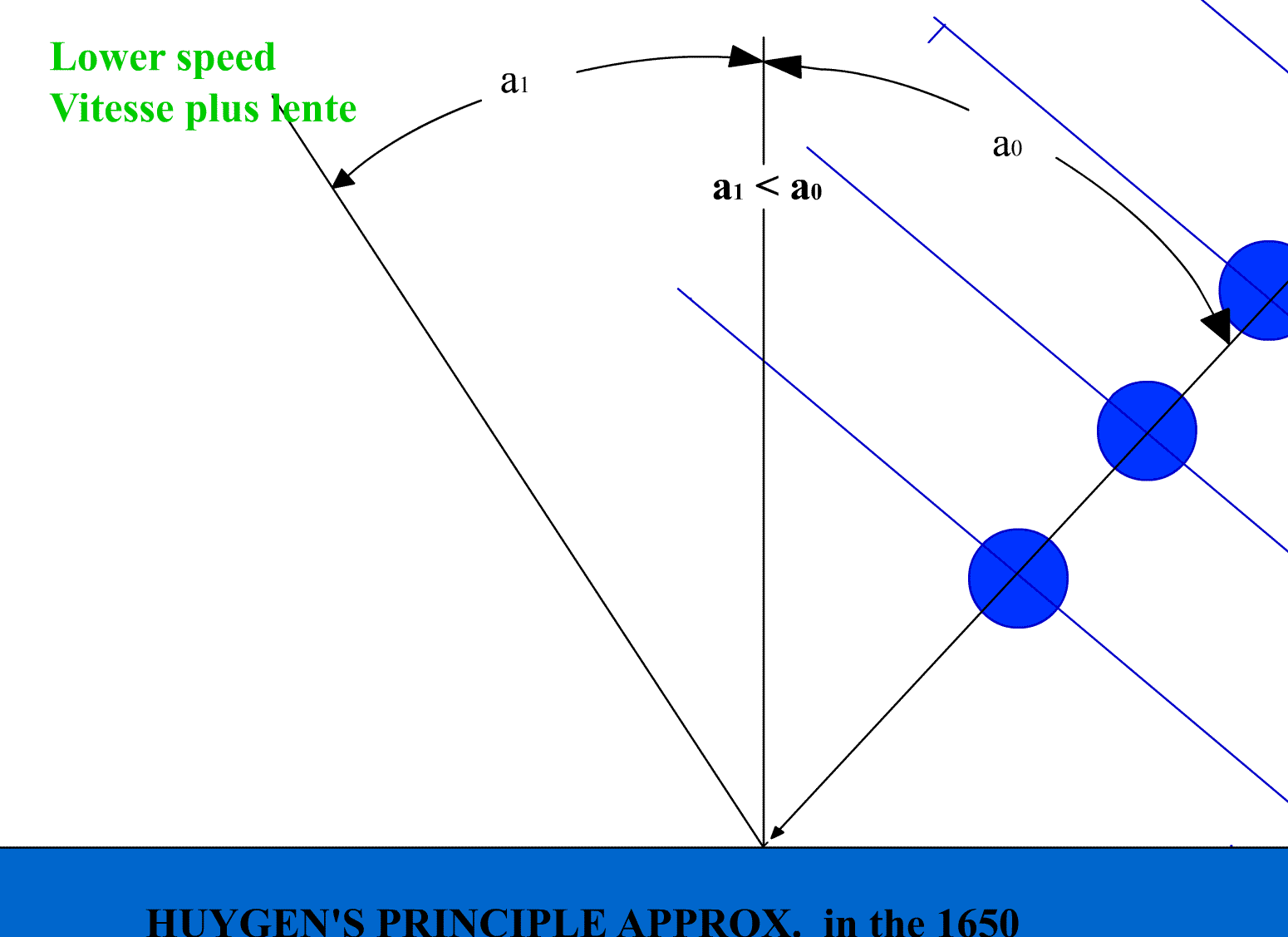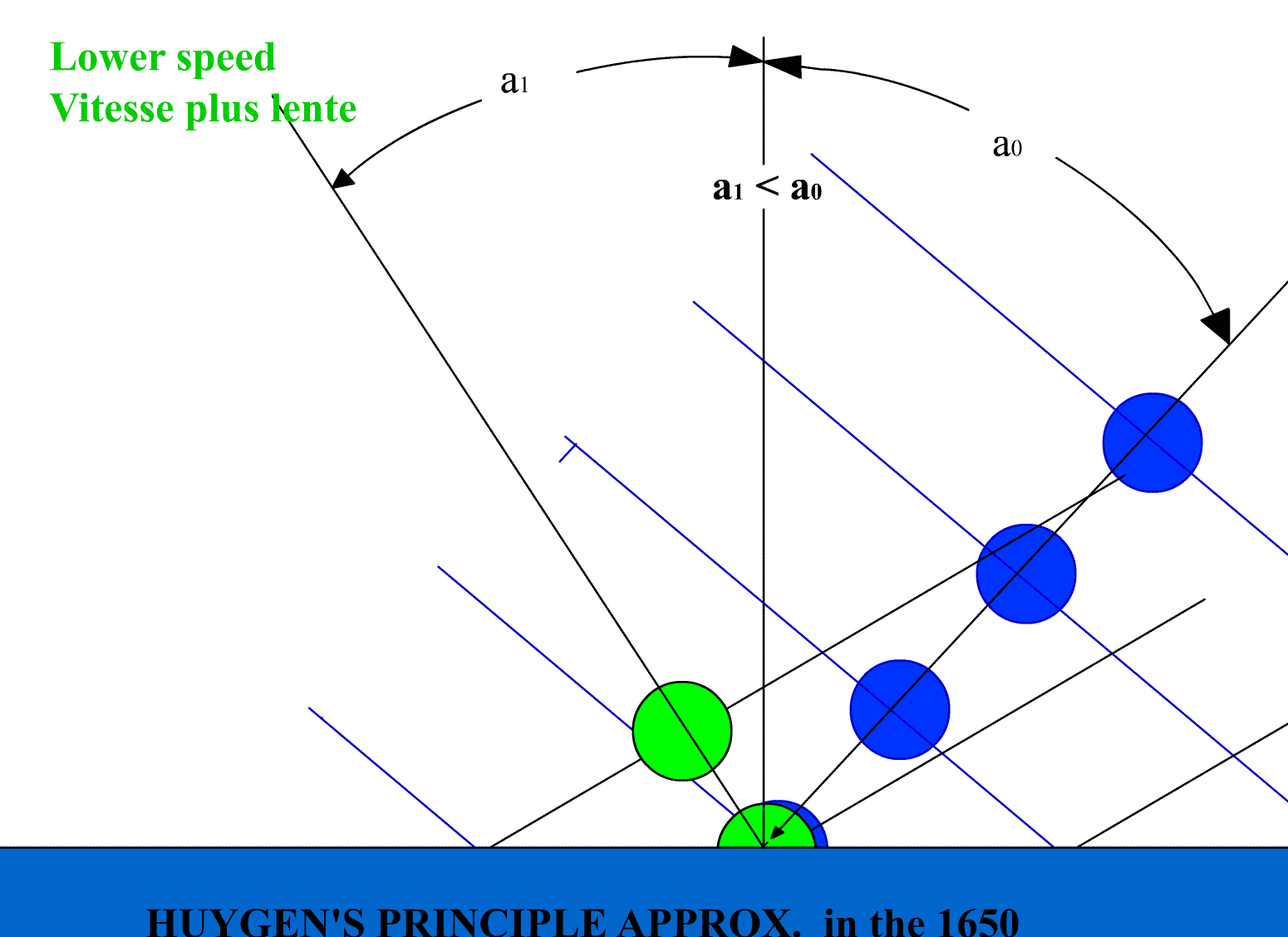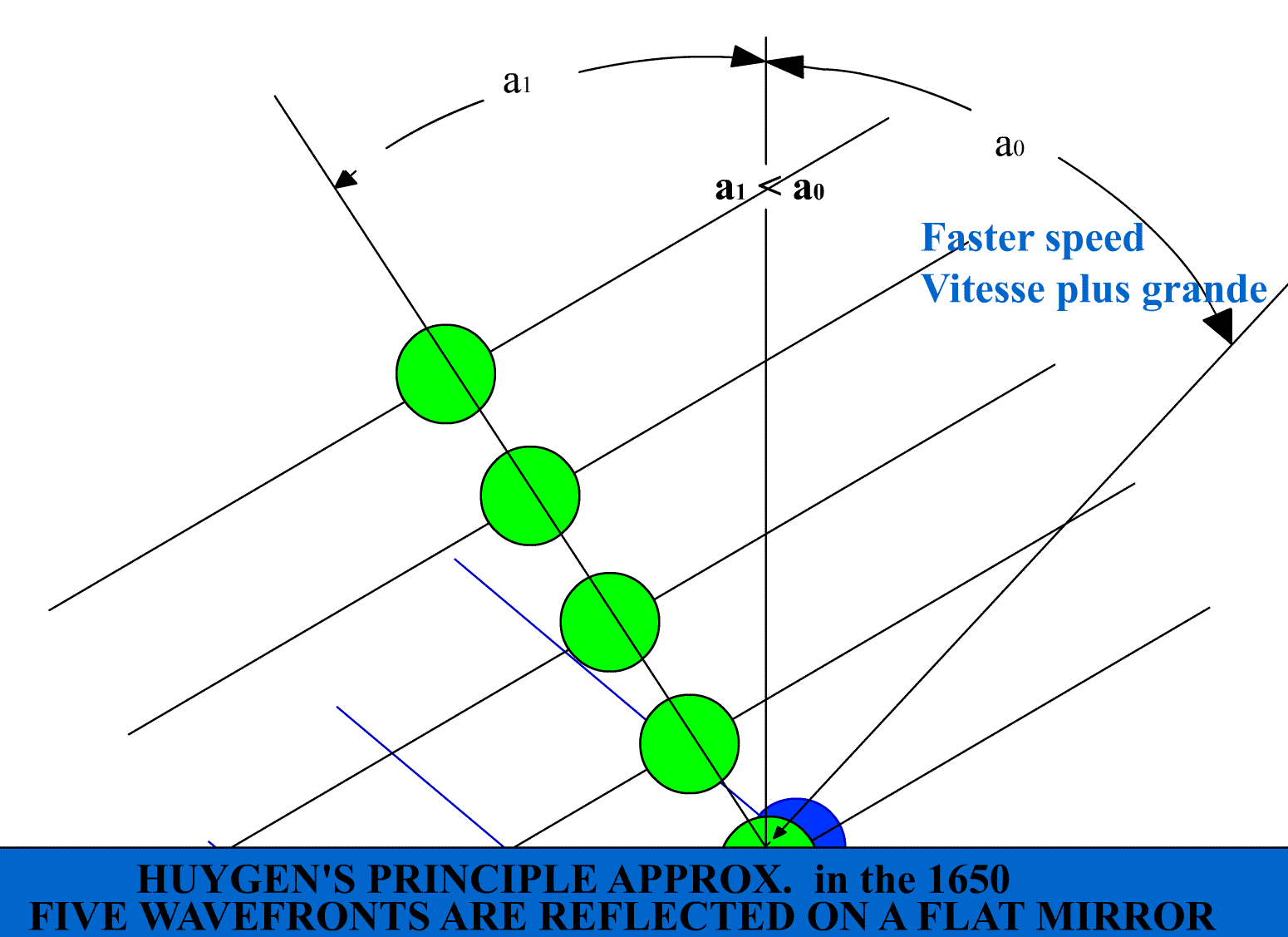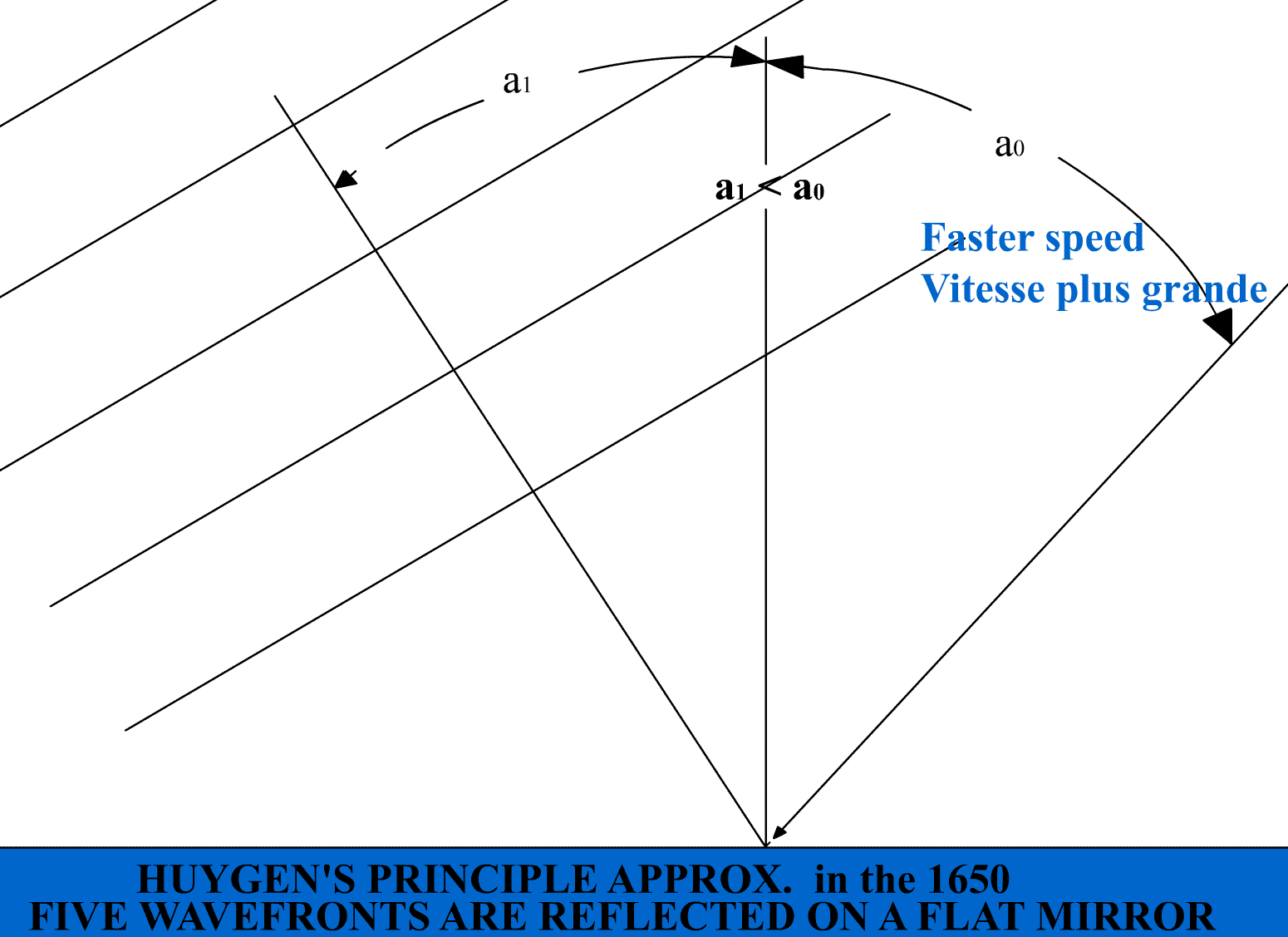
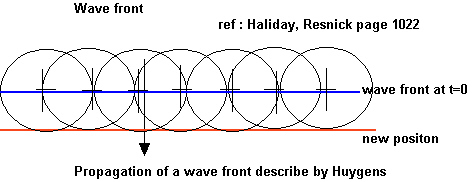
B) Wave theory shows displacement of focal point with a speed shift in reflection

i) Huygens' Theory for a wave front :

All points on a wave front can be considered as point sources for the production of spherical secondary wavelets. After a time "t" the new position of the wave front will be the surface of tangency to these secondary wavelets. The theory was accepted because it can predict the well established laws of reflection and refraction.

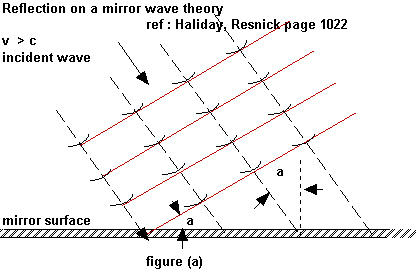
ii) The law of reflection based on Huygens' theory for light travelling faster than the speed of light "c":

1) Diagram showing incident light before it falls on the mirror

Figure a) just below, shows four waves fronts falling on a mirror along with its associated rays selected at random . For convenience the waves are chosen to be one wavelength apart. Note that (a), the angle between the wave fronts and the mirror, is the same as the angle between the incident rays and the normal to the mirror. In other words, "a" is the angle of incidence.

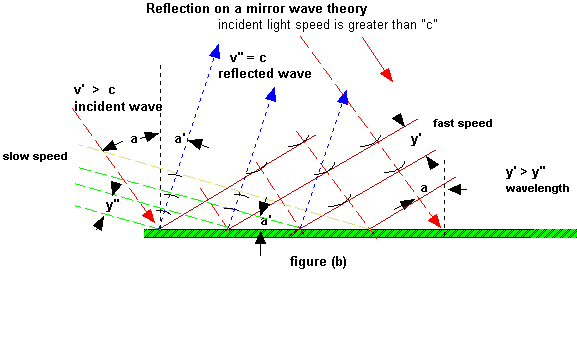
2) Reflection on a flat mirror for light travelling faster than the speed of light "c":

Figure b) we show the waves in yellow being reflected on the mirror surface. Notice the change in wavelength after reflection because of the speed shift. (a')is the angle of reflection. It is the angle between the reflected wave fronts in yellow and the mirror or the angle between the reflected rays in blue and the normal to the mirror. Normally the reflected angle is the same as the angle of incidence because the speed of light in our reference system is a constant "c" = 300 000 km/sec.

But here we have light coming in our reference system from an other system at a speed of say 312 000 km/ sec. The incident light remains at 312 000 km/sec until it falls on the mirror. Because of Michelson's experience the reflected speed becomes 300 000 km/sec as soon as it interfere with the mirror surface.

3) Reflection on a spherical mirror

Let see now what happens when we apply Huygens law to a spherical mirror in space. In Figure b) When we build Huygens'diagram the geometry impose that the angle of reflection (a') must be less than the incident angle (a). This is cause by the change of the light speed.
Since the flat mirror shown in green is a macroscopic portion of a spherical mirror, the normal to the mirror correspond to the radius of curvature of the sphere. As you can see on the following diagrams, the reflected rays tend to shift towards the radius. This is why the image formed is blurred, the image forms away from the normal focal point. The shift is given by the following formula: sin (a) / sin (a') = V' / c . From the formula we can calculate the speed of light coming from space based on the displacement of the focal position. At the end we give you the details of the calculations conducted for the Hubble's telescope in section "Calculation"

Ref.#7-a) (Reflection angle is not always the same )
Ref.#7-b) (Curved surface is made up of flat surface)