
Planetary spectroscopy and photometry are different domains than star spectroscopy and photometry. As we are looking to objects whose perceived light is merely reflected sunlight (at least at wavelengths accessible to amateurs), for studying them it is interesting to calculate how much light they scatter back from the total flux received from the Sun. This is called the albedo. Albedo can be calculated either from spectroscopic or photometric data. Here is how I have calculated the albedo of the planet Neptune from data obtained on August 22nd, 2019.
The
photometric albedo of Neptune
On
the way I learned to calculate albedo, this is the first step.
Calculating photometric albedos will give us one parameter mandatory to
calculate the spectroscopic albedo. The idea there is to calculate how
much light is relfected by the planet through each one of the
photometric Johnson band.
First, it is necessary to calculate the normalized magnitudes of Neptune (page to be written). Normalized magnitudes calculate the brightness of a Solar System object as if it was located at one astronomical unit (AU) from the Sun, and one AU from the Earth. Here are the calculated values for Neptune on August 22nd, 2019:
| U |
B |
V |
R |
I |
|
| Apparent magnitudes |
8,46 |
8,13 |
7,73 |
7,73 |
8,45 |
| Normalized
magnitudes |
-
6,27 |
-
6,56 |
-
6,96 |
-
6,96 |
-
6,25 |
(Let's not comment the results here, I'd just say that B and V are reliable, R and I a bit less, U not really). The geometric albedo for each color band is given by the formula found in the book by Richard Schmude, Uranus, Neptune, Pluto and how to observe them (Springer, 2008):
Geometric
albedo = 10exp(0,4 x (SUN_Nm - NEPT_Nm) - 2 X LOG (SIN Ϭ)
Where Nm means "Normalized magnitude" and Ϭ is the angular size of the radius of the target at a distance of 1AU in degree. To calculate Ϭ R.Schmude gives for Neptune the formula:
Ϭ = 0,009403 - (6,814 x 10E-8) x s + (2,602 x 10E-8) x s²
Where
s is the sub-Earth latitude on Neptune at the moment of the observation
(s = -23,7 here). I have used more recent values for the magnitudes of
the Sun than those given in the book, found in Willmer, 2018, The absolute magnitude of the Sun in several
filters. And now these are the values of albedo of Neptune
and the values used for the Sun:
| U |
B |
V |
R |
I |
|
| SUN normalized magnitudes |
- 25,97 |
- 26,13 |
- 26,76 |
- 27,15 |
- 27,47 |
| Neptune
geometric albedo |
0,49 |
0,55 |
0,44 |
0,31 |
0,12 |
The
B and V values are in good coherence with Schmude's results (The secular and rotational brightness variations of
Neptune, 2016) ; R and I look higher, while U is definitely wrong
(it should be around 0,57).
The
spectroscopic albedo of Neptune
The formula to calculate the spectroscopic albedo is found in Erich Karkoschka's Icarus paper (111, 174-192 - 1994) : Spectrophotometry of the jovian planets and Titan at 300 to 1000 nm wavelength: the Methane spectrum:
Albedo = (Δr/Ϭ)² x (Neptune ADU spectrum/ Sun ADU spectrum)
Where
Δ and r are respectively the
geocentric and heliocentric distances of Neptune.
We
start from the reflectance spectrum of Neptune. This is simply the
uncorrected spectrum of Neptune divided by the uncorrected spectrum of a
solar analog star taken under the same conditions. The star I have used
as reference is HD217877 in Aquarius ; this is a G0V star, a little
different from the Sun (slightly more intense in blue, slightly less in
red). The resulting reflectance spectrum so far has no objective
intensity scale:

To obtain the albedo spectrum, we need to turn the spectrum of the G0V star into a spectrum that is equivalent to that of the Sun. This has been done in three steps. First, I have recalculated the photometry of the star, in order to increase the accuracy. The V mag of HD217877 has been found to be V = +6,75 with a B-V of +0,59. This is 0,07 mag fainter than the SIMBAD value, which is noted to be of poor quality (E). But the color index is coherent (SIMBAD = +0,58) so we can adopt the new value. The next steps are the following:
| 2) To increase again the
accuracy, I had the idea to bring a small correction to the
profile of HD217877. By dividing the theoretical G0V profile by a
theoretical G2V profile, is obtained a coefficient spectrum which
highlight the differences between the two very close spectral
types. The original G0V ADU spectrum is divided by the coefficient spectrum. Then we get the same spectrum with a slightly corrected profile even closer to that of the Sun. We can see that the new profile is less intense in the blue part, but more intense in the red part, as it should be. |
 |
| 3) The next step is to
correct the intensity of the modified HD217877 spectrum, so it
matches the intensity that the Sun itself would have. First, we
need to calculate how brighter is the Sun in comparison with
HD217877. Here is the formula: Mag-diff
= 2,512exp(V_HD - V_Sun)
Mag-diff
= 2,512exp(6,75- (-26,75))
Mag-diff
= 2,542E+013
So the Sun is 2,542E+013 brighter than HD217877 (33,511 magnitudes). The spectrum of the star is multiplied by this value. Now we get a pseudo-Sun ADU spectrum. The profile is slightly smoothed to erase the small-scale noise brought by the original division by the G0V/G2V coefficient. |
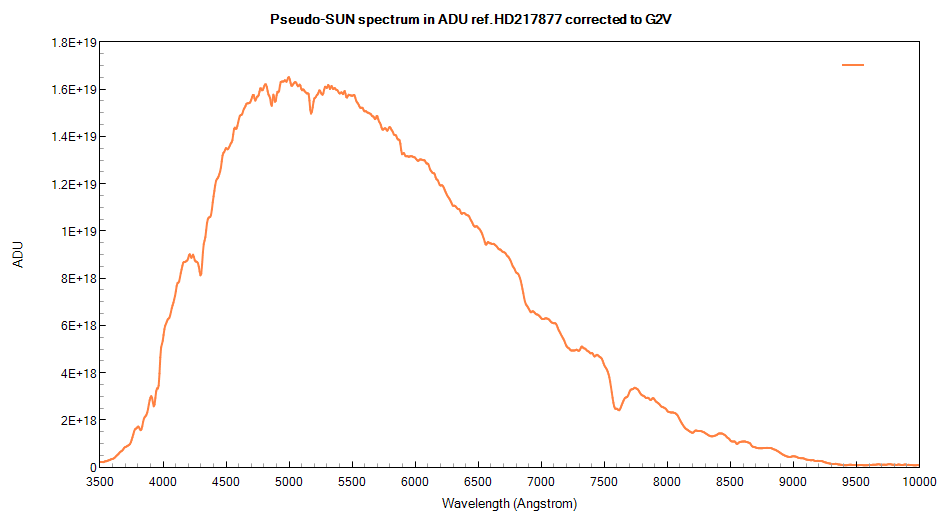 |
| 4) The final step is to
divide the ADU spectrum of Neptune by the ADU spectrum of the
pseudo-Sun. Then, following the formula described earlier by
E.Karkoschka, we multiply the reflectance spectrum by the (Δr/Ϭ)²
factor (which is equal there to 2,784E+013). Now, the intensity
scale of the spectrum represents the albedo value. The calculated profile is coherent with that obtained by E.Karkoschka, with a value around 0,55 in blue light and between 0,05 and 0,2 in infrared. It is also coherent with the B and V photometric albedos calculated at the beginning (see below) |
 |
Below
is the albedo spectrum with the photometric albedo values.
