Bruno-

Voilà ! Pour moi c'est ça le principe n° 1. Je dirais même : si ça fatigue la vue, il faut arrêter (et être ébloui fatigue la vue). Attention à ne pas interpréter de travers les conseils. Ceux qui clament que la Lune peut s'observer sans filtre, que c'est sans danger, etc. précisent (normalement) que oui, mais de jour ou bien avec un éclairage important. Mais pas juste « c'est sans danger ». Moi, dans le noir, la Pleine Lune à faible grossissement m'éblouit, donc fatigue ma vue, donc je mets un filtre (ou je grossis plus fort). Ça se trouve c'est vraiment sans danger dans tous les cas, JML a sûrement raison, je m'inquiète pour rien. Mais ça me fatigue, ça me fait pour ainsi dire mal aux yeux, alors où est le plaisir ? La vue, c'est ce qu'on a de plus précieux. Mieux vaut avoir peur inutilement que la fatiguer.

(Discussion hors sujet sur le précision de la mise en station requise en visuel) MCJC : je faisais du « jeté de monture » aussi pour les observations planétaires à x300. Je me souviens que, au sud, les planètes restaient dans le champ de l'oculaire quand je faisais une pause d'un quart d'heure, mais pas d'une heure : c'est seulement au chercheur que ça restait. Ce dessin de Saturne a été fait avec le 300 mm sur EQ6, à x300, avec le « jeté de monture » : (Lally : c'est fait avec un 300 mm quand Saturne était haute dans le ciel. Saturne sera visible en automne prochain, mais bien plus basse, et en plus ses anneaux seront presque fermés, donc ce sera plus difficile de la détailler.) (Ah, ben j'ai un dessin au Dobson 495 mm avec les anneaux presque de profil : http://www.astrosurf.com/bsalque/Dessins/maj/saturne1402.jpg . L'automne prochain elle ressemblera à ça. Ensuite, les années qui suivront, elle sera de plus en plus haute dans le ciel et ses anneaux vont s'ouvrir, mais de l'autre côté. C'est ça qui est génial avec les planètes : année après année, on les voit sous tous les angles, dans toutes les configurations possibles...) Pour moi, ce qui est décisif, c'est de passer d'une monture manuelle à une monture motorisée. Même si je ne faisais pas de vraie mise en station, c'était nettement plus simple d'observer à fort grossissement, même si de temps en temps il y avait un petit rattrapage à faire. Mais le pas décisif, c'est la motorisation. Bon, si je faisais une vraie mise en station, je n'aurais plus ces petits rattrapages, mais ce n'est pas important. (Aujourd'hui ce télescope est utilisé en Dobson pour d'autres raisons qui l'emportent sur le confort de la motorisation : observation assis, facilité à installer et transporter.) Encore une fois, en visuel il n'y a rien à faire (juste orienter le trépied). Tu parles d'application sur ordiphone, de régler sur la Polaire... pfou, c'est trop compliqué pour moi

OK, en fait ça dépend ce qu'on appelle mise en station. Quand j'utilisais mon 300 mm sur une monture EQ6 (donc motorisée), je n'ai jamais fait de mise en station. Un jour j'ai regardé dans le viseur polaire par curiosité, mais je ne l'ai jamais utilisé. Ce que je faisais : je regardais où est la Polaire, OK elle est là ; je posais le trépied de façon à ce que le pied nord soit dirigé vers la Polaire (sachant que l'axe de la monture avait été réglé une fois pour toutes pour une latitude entre 45° et 50° − celle de chez moi) et c'est tout. C'était suffisant pour profiter du suivi motorisé. Je n'appelle pas ça une mise en station (j'aime bien l'expression « jeté de monture »). Je suppose que, au contraire, tu appelles ça une mise en station. Mais ce qui est important, c'est de comprendre que cette « mise en station » simpliste suffit. Il n'y a donc aucune complication supplémentaire à faire du visuel avec une monture équatoriale.

Le lien que j'ai donné décrit un Maksutov 90 mm sur monture équatoriale (si si) non motorisée. C'était un exemple, je ne tiens pas spécialement au modèle équatorial ou à l'azimutal, pour moi peu importe. Justement, j'avais proposé à Lally de regarder dans d'autres magasins les différents modèles qui existent (équatoriale, azimutal...). Ces télescopes sont légers, faciles à transporter, et demandent une vraie monture (à cause des forts grossissements), voilà ce qui me semble important. Pas pour l'observation visuelle, il faut juste orienter l'axe de la monture vers le nord (mais ça n'a pas d'importance puisque le modèle motorisé coûte plus cher, il me semble que c'est hors-sujet).

Les petites montures équatoriales, elles sont parfaitement utilisables pourvu que le tube ait un poids adapté. J'ai utilisé plusieurs années un 115/900 sur sa petite monture équatoriale, c'était plus stable que la plupart des petites lunettes azimutales. Et en effet il n'y a pas besoin de faire de mise en station, juste de poser la monture dans la bonne direction (axe de la monture pointant vers la Polaire, en gros). MCJC : je trouve que tu anticipes trop sur le futur. Lally a un petit budget, il me semble donc inutile de se demander si ton télescope sera évolutif. Pourra-t-on plus tard faire de la photo, installer de grosses jumelles ou un C6 ? Pour moi, ce genre de question va parasiter le choix, surtout qu'il n'y en a pas tellement (de choix). Par exemple tu dis que même si la monture supporte le Maksutov 90, c'est une mauvaise idée. Ben si, c'est une bonne idée, puisqu'elle supporte le télescope. Tu as l'air de penser que les gens gardent leur première monture quand ils passent au diamètre supérieur ou se lancent dans la photo. Mouais. Pas tout le monde en tout cas. De toute façon, plus tard c'est plus tard, on verra. À mon avis le choix de Lally devrait se faire en fonction des prix. Peu importe que le Maksutov 90 mm soit azimutal ou équatorial, ce qui compte est qu'il rentre dans ses prix. Un Maksutov 90 azimutal est une très bonne idée pour débuter à bas prix avec un instrument facile à transporter. Un Maksutov 90 équatorial est une très bonne idée pour débuter à bas prix avec un instrument facile à transporter.

Pour moi c'est le contraire : Lally doit commencer le plus tôt possible, parce que rien ne vaut la pratique. Quand j'ai débuté avec ma lunette de 60 mm, j'ai pris ce qu'il y avait dans le budget et je me suis adapté. Je ne regrette pas d'avoir démarré sans aucune connaissance, sinon j'aurais perdu du temps. Mais on n'a pas tous les mêmes expériences, bien sûr.

Le lien que j'ai donné est celui de magasin Optique Unterlinden, en effet importateur de Skywatcher. Si tu peux patienter jusquà janvier prochain, ils sont très réputés pour leurs soldes (le seul magasin à ma connaissance à faire de vraies soldes sur le matériel astro). Si tu cherches un magasin spécialisé pas loin de chez toi, il y en a peut-être. En général tous les magasins astro se valent et sont dignes de confiance (et en général ils sont gérés par des astronomes amateurs). Si le Maksutov 90 mm te paraît le bon choix, je te recommande de regarder les différents modèles qui existent. Mon exemple n'était qu'un exemple. Outre les magasins déjà cités, j'aime bien L'Astronome parce que je trouve son site très pratique ( https://www.astronome.fr/ ). Si tu commandes en ligne en payant avec ta carte bancaire, c'est forcément sécurisé, mais du côté de la banque, puisque (il me semble) la loi oblige toutes les banques à utiliser une double sécurité.

C'est le contraire. C'est l'inexistence de la matière noire qu'il faut prouver. J'explique mon point de vue (ce n'est que mon point de vue d'astronome amateur, hein). Je rappelle qu'il y a deux alternatives. 1) On postule que la théorie de la gravitation est juste, alors les observations impliquent l'existence de matière invisible, qu'on appelle la matière noire. Qu'il existe de la matière invisible n'a absolument rien d'extraordinaire, c'est le contraire qui le serait. Un univers où toute la matière émettrait des photons me paraît complètement fantasmagorique, on dirait un mythe religieux, vous ne trouvez pas ? Au passage, je rappelle que la découverte du neutrino est similaire. J'ai relu Wikipédia et je vous cite des passages : « En 1930, la communauté des physiciens est confrontée à une énigme : la désintégration β ne semble pas respecter les lois de conservation de l'énergie, de la quantité de mouvement et du spin. Pour satisfaire ces principes, Wolfgang Ernst Pauli postule l'existence d'une nouvelle particule, de charge électrique nulle » La matière noire, c'est pareil, sauf que c'est son rayonnement qui est nul. « Le neutrino [...] est découvert expérimentalement en 1956 » Je soupçonne qu'on attendra plus de vingt-six ans avant de « voir » (ce qui est impossible) la matière noire. Tiens, et les trous noirs ? C'est pareil, on n'a pas de preuve directe, personne n'en a vu un, ce qu'on voit, c'est juste ce qu'il y a autour, c'est le même principe : si la théorie est juste, elle implique l'existence des trous noirs. 2) On postule que la matière noire n'existe pas (pourquoi donc ? et les trous noirs ? bizarre, mais OK, admettons...) et alors il faut changer la théorie. L'alternative 1 est l'alternative « normale », en vertu du rasoir d'Ockham disons, et l'alternative 2 est l'alternative « révolutionnaire » (la théorie de la relativité générale serait incomplète !), c'est pour ça que c'est son postulat qu'il faut prouver. Jusqu'à preuve du contraire, notre théorie de la gravitation est juste, donc il y a de la matière noire dans l'univers.

Superbe dessin, parfaitement ressemblant !

Les grosses jumelles ne sont pas polyvalentes, en particulier elles ne permettent pas d'observer les planètes (juste de les voir, mais sans rien dessus), et ce sera trop limité sur la Lune. Ces instruments sont faits pour le ciel profond à grand champ, qui se pratique sous un ciel bien noir, donc peut-être pas à côté de la maison. Alors qu'un petit Maksutov 90 mm montre tout ce qu'il faut pour découvrir le ciel : les cratères de la Lune (et par paquets), les caractéristiques principales des planètes (les phases de Vénus, la calotte de Mars, les bandes équatoriales de Jupiter, les anneaux de Saturne) et même un peu de ciel profond (pas la nébuleuse de la tête de Cheval, bien sûr, mais la nébuleuse d'Orion et les grands amas ouverts). Le point fort de cet instrument, c'est plutôt les forts grossissements (qui ne seraient pas permis par une lunette courte). Donc il faut une monture stable avec des mouvements micrométriques. Ce serait bête d'avoir un télescope de bonne qualité optique (l'autre point fort, c'est sa qualité optique tout à fait correcte, que je soupçonne supérieure à celle des Newton 130 ou 150 mm) et de ne pas exploiter cette qualité optique. À un moment donné il faut assumer : soit on choisit un instrument facile à transporter, mais limité (jumelles, lunette courte − ce n'est pas polyvalent), soit on fait l'effort de monter les escaliers avec une petite charge. Lally : tu as déjà grimpé les trois étages avec un pack de bouteilles d'eau (9 kg) ? Si oui, un « vrai» télescope est à mon avis envisageable. En neuf, ça dépasse le budget : https://www.telescopes-et-accessoires.fr/telescope-sky-watcher-mak-90-sur-monture-starquest-c2x30355945 Mais c'est de la qualité. (Un avantage auquel je n'avais pas pensé : sa relative longue focale permet d'avoir un fort grossissement avec l'un des deux oculaires livrés (x125). Inutile d'acheter un troisième oculaire comme c'est le cas par exemple avec les Newton.)

Oui, tu l'as dit plus haut quand tu as posté les photos. C'est pour ça que je parle de la contrainte de descendre avec le matériel. Si tu observes à côté de la maison, il me semble que le plus contraignant, ce sera de descendre les trois étages. Est-ce que tu te vois faire deux voyages pour t'installer en bas ? Si tu penses que ça va être compliqué, il faudra peut-être envisager quelque chose de très léger, transportable en un seul voyage. Est-ce que des Astrosurfeurs par ici ont ce genre d''expérience ? (Lors de la décennie précédente, j'habitais au troisième étage d'une petite résidence. Je descendais le Dobson 300 mm en trois voyages : le socle, le tube, les accessoires. Ben je ne sortais pas souvent...)

J'ai relu... Tu parles d'un jardin, donc tu pourras observer au pied de la maison ? Si oui ça m'a l'air peu contraignant vis à vis du transport, sinon qu'il faudra descendre le matériel. Bref, je me range à l'avis de Grelots. Un Maksutov 90 mm est léger, pratique d'utilisation, à part qu'on n'aura pas accès à de très faibles grossissements, ce qui rendra le pointage plus difficile. Mais ce sera plus facile à transporter, je pense notamment aux escaliers.

Oui, il faut plutôt parler du transport globalement : quel moyen de transport, sur quelle distance, et avec quelles contraintes ? Si Lally n'a pas de voiture et compte rejoindre le site d'observation à vélo, même avec un petit budget il faudra éliminer certains instruments.

Pourquoi ça ? À cause de : MCJC a entièrement raison, je ne comprends pas pourquoi on chipote sa réponse (il est possible qu'on voie la Lune lorsqu'elle sera à haute déclinaison, mais seulement certains jours dans l'année, et à un moment bien précis de la nuit ; ce sera rare, trop pour miser sur le balcon). Donc on cherche un instrument transportable. Le site d'observation sera loin ?

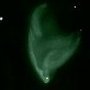
C'est une photo longue pose. Tu peux espérer un jour faire ce genre de photo. Mais tu ne verras jamais ces couleurs. Au mieux, si l'instrument est suffisamment puissant et si ta vue est sensibles aux couleurs nocturnes, tu verras une nébuleuse verte. Voici un dessin avec un télescope de 210 mm : C'est ce qu'on voit à l'oculaire de ce télescope, mais le vert est quand même plus subtil. Cette teinte, je l'ai vue dans un 115/900, mais je sais que pour la majorité des observateurs il vaut mieux au moins 200 mm de diamètre. Mais même en noir et blanc, quel plaisir de découvrir cette nébuleuse au sein de laquelle naissent de nouvelles bébés-étoiles ! ----------- Tout à fait ! Mais c'est dans un deuxième temps qu'on découvre son véritable « destin ». Au début, il faut tout essayer, d'où l'intérêt d'un instrument d'initiation polyvalent.

Lally : mon précédent message n'avait pas vocation à être désobligeant, mais réaliste. Du coup j'aurais peut-être dû être moins abrupt, désolé... Je vois que tu es noyée sous les conseils. Je vais récapituler les choses importantes. Tu noteras que je ne suis pas d'accord avec tout le monde, mais je suis sûr d'avoir raison (comme les autres...) et, surtout, je vais expliquer pourquoi. 1) L'astronomie s'apprend. Et le mieux pour apprendre, c'est de pratiquer. Achète un télescope ou une lunette à 200 € et utilise-la/le. Ce sera de l'entrée de gamme ? Super : mieux vaut débuter sans se ruiner. Certains te diront que c'est mieux d'attendre un peu pour gonfler le budget. Je ne pense pas que ce soit la meilleure idée. Quand comme toi on a attendu trente ans, il est temps de s'y mettre ! 2) Le choix de l'instrument n'a pas tellement d'importance. Une lunette 90/900, un télescope 130/900, un Maksutov 90 mm : ce sont d'excellents choix pour découvrir le ciel (sauf si tu choisis une marque de supermarché, genre National Geographic). Voilà des valeurs sûres. Si tu envisages autre chose, parles-nous en d'abord. (De plus ton budget est trop faible pour un instrument électronique. Pas grave, on est nombreux à être restés aux instrument manuels.) 3) Le choix des observations souhaitées n'a aucune importance : avec ton budget, tu n'auras pas le choix, tu observeras ce que tu pourras, et c'est déjà très bien. J'ai débuté avec une lunette 60/700 et j'en garde de merveilleux souvenirs, y compris lorsque je ne trouvais pas les cibles. C'est normal : j'étais en phase de découverte (alors qu'aujourd'hui, je ne peux plus me passer d'un grand diamètre). 4) Ce qui est important, ce sont les critères pratiques. Exemple : est-ce que tu as un grand balcon ? Ce n'est pas pour être indiscret, mais pour savoir si tu pourras déployer le trépied d'une lunette de 90/900 (ces lunettes ont besoin d'être positionnées hautes, puisqu'on observe du côté le plus bas, donc le pied doit être déployé sur une grande largeur). Ton site d'observation (balcon, jardin, etc.) est orienté comment ? Ce n'est pas pour être indiscret mais parce que le ciel s'observe essentiellement vers le sud : c'est là que les astres culminent, donc sont observables dans les meilleures conditions. Si le site est orienté vers le nord, il faudra changer de site, et ce ne sera peut-être pas simple. Est-ce que tu as une voiture et comptes-tu l'utiliser pour te rendre sur le site d'observation ? Ce n'est pas pour être indiscret, mais pour savoir si tu pourras envisager un instrument encombrant (genre un Dobson 200/1200 d'occasion). En fait, un bon instrument est un instrument qui te convient, pas qui nous convient. On a donc besoin de t'imaginer en situation, et d'en savoir plus sur tes contraintes ou tes habitudes. 5) Si tu as trop d'attentes, tu risques d'être déçue, quel que soit l'instrument. La Lune est merveilleuse même avec un instrument d'entrée de gamme, mais les planètes seront toutes petites (elles sont toujours plus petites qu'on ne s'y attend, toujours) et les objets du ciel profond ne montrent pas de couleurs − en ville ils seront quasiment tous invisibles, en gros. Il est donc très important de progresser en science astronomique en même temps qu'on progresse en observation. Quand je débutais avec ma lunette de 60/700 je ne voyais pas grand chose. Mais je suivais l'actualité astronomique (en étant abonné à un magazine). Lorsque l'astéroïde Cérès est passé, j'ai pu l'observer : j'ai vu une étoile parmi d'autres, mais il avait bougé quelques jours plus tard. Aucun intérêt esthétique, mais un excellent souvenir d'observation ! Tu vas devoir digérer beaucoup de conseils. Ne lis pas nos affirmations, juste nos arguments, et essaie de te reconnaître dans les arguments.

Lally semble débutant. Quand on débute, on ne sait pas quelles observations on veut faire. Par exemple il est fréquent que des débutants disent qu'ils veulent faire du planétaire parce qu'ils croient que le ciel profond n'est pas adapté à des novices (c'est faux). Donc quand Lally dit vouloir voir les cratères de la Lune, je l'interprète comme « j'ai un petit budget, je sais que ne je verrai pas grand chose, mais j'aimerais voir quand même des cratères sur la Lune ». En fait, quand on aime l'astronomie, surtout au début, on veut tout voir. C'est pourquoi je crois qu'il ne faut pas trop se focaliser sur la demande précise de Lally (d'autant que tous les instruments d'astronomie permettent d'observer les cratères lunaires en détail (à part les jumelles). Ce qui est important, ce n'est pas de savoir quels cratères il veut observer (le comble de la spécialisation !) mais quelles sont ses conditions d'observation (le balcon, c'est pas terrible sauf s'il est spacieux, mais Lally a dit pouvoir sortir... où ? en ville ? en rase campagne ?)

Celui fourni est de l'entrée de gamme, mais il est utilisable en attendant. Par contre en général il ne fournit pas un grossissement assez fort, donc ta remarque est juste : il faudra acheter un oculaire supplémentaire. Mais autant attendre si le budget est serré : mieux vaut une lunette de 90 mm avec deux oculaires bas de gamme (on achètera le troisième plus tard) qu'une lunette de 70 mm avec trois oculaires dont un bon. Tout à fait d'accord sur les autres points, notamment le point 1 (ces télescope sont parfois tellement mauvais qu'ils sont inutilisables, c'est autre chose que les oculaires d'entrée de gamme).

Parmi les instruments cités, je dirais que les meilleurs choix sont la lunette 90/900 et le Maksutov 90 mm. En occasion, on peut peut-être avoir un plus grand diamètre, c'est toujours utile (c'est le diamètre qui compte). Lally : tu comptes observer en ville ? dans un village ? en rase campagne ? C'est pour savoir si tu peux envisager les observations stellaires (et notamment le ciel profond) ou seulement la Lune et les planètes.

Attention, tu vas tomber dans le panneau du marketing. Parler de télephone intelligent (ou smartphone) ou bientôt d'oculaire intelligent, c'est du marketing. Il existe un mot peu utilisé mais parfaitement adéquat : ordiphone. En effet, les ordiphones sont bien constitués à la fois d'un ordinateur et d'un téléphone. Pour ces oculaires, je ne sais pas ce qu'on peut dire. Il existe des télescopes connectés (comme l'Evscope), mais je ne sais pas si ces oculaires sont connectés. Il me semble qu'il s'agit à base d'un oculaire numérique avec, comme nouveauté, l'intégration d'un logiciel (notamment pour prétraiter les images). Donc un ordiculaire ? Bof. Un oculaire électronique avec logiciel intégré me paraît convenir mais c'est peut-être un peu long. Mais, pitié, pas la novlangue du marketing !

« God's favorite galaxy » est dans l'amas Perseus, j'ai l'impression (elle ressemble à la galaxie d'Andromède, ce qui n'a rien d'extraordinaire). Enfin une piste pour trouver de la vie extra-terrestre ! (Je ne m'attendais pas à ce qu'on en trouve d'aussi proche.)

Pour les réduire, on peut rester au coulant 31,75 mm et ne pas utiliser de Barlow. C'est ce que j'ai fait (je suis feignant...) ------------ Sinon, comme déjà dit plus haut, faire de l'astrophoto ne signifie pas rester debout. Quand on lance des poses de 2 minutes pendant une heure, on peut même aller faire une petite sieste en attendant... (Bon, normalement on reste à coté pour surveiller). Par contre, il est vrai que pour manipuler l'appareil photo avec un Newton équatorial, il faut être debout. Mais ce n'est pas le cas avec une petite lunette, ou un Schmidt-Cassegrain. C'est d'ailleurs pareil en observation visuelle : selon les instruments, on peut avoir besoin d'être assis ou debout. Ça dépend de l'instrument, pas de visuel vs photo.

Et tu en as retenu quoi ? Si j'ai bien compris, tu sais que tu ne feras pas d'astrophoto, c'est une information importante. Parmi tous les appareils que tu as utilisés, certains t'ont-ils plu plus que d'autres ? Est-ce que tu préfères observer debout plutôt que assis ou le contraire ? Tu as pu voir l'installation et les réglages, est-ce que ça t'inspire quelque chose ? (Oui, j'étais inquisiteur dans une vie antérieure ) Correction : tu ne veux pas de matériel d'initiation pour ton télescope définitif. Mais je parlais d'un télescope à acquérir dans un premier temps, afin d'emmagasiner de l'expérience avant de dépenser le gros pactole. Mais bon, compte tenu de ton expérience en club, ce n'est peut-être pas utile. En tout cas, ce que j'ai retenu de la discussion : − tu as le temps − pas de photo, − site d'observation accessible facilement sous un très bon ciel (il faut juste traverser une terrasse en béton avant d'atteindre le jardin), − télescope pilotable par informatique (c'est bien pour ça que tu parlais du Synscan ?) Est-ce que tu te vois transporter un Dobson de 300 mm, éventuellement démontable ? (Donc 2 morceaux pas trop lourds, mais ensuite il faut le monter.) Si oui, un Dobson 300 mm goto me semble répondre au cahier des charges, et avec un tel diamètre tu t'en mettrais plein la rétine. Mais d'autres choix sont possibles. Ne tiens pas compte des réponses mais des arguments. (Ndesprez : n'hésite pas à détailler, même s'il semble y avoir une majorité de gros télescopes par ici... justement !)

Bonjour Walter957 ! Tu n'as jamais fait d'observation ? Dans ce cas il y a un gros risque que tu dépenses ces 1800 € à mauvais escient. Le matériel est très diversifié parce que la pratique l'est. Le mieux, je trouve, c'est de commencer avec du matériel d'initiation. Ce matériel va permettre d'acquérir une première expérience, et c'est suite à cette expérience que tu connaîtras mieux tes besoins et sauras vers quoi te diriger. Nous, on ne peut pas deviner (et toi non plus au début, sauf si tu sais à l'avance ce qui te plaira, situation rare). Mon conseil : achète un petit instrument d'occasion, pas cher, n'importe lequel pourvu qu'il soit de qualité correcte (pas d'instruments de supermarché), utilise-le pendant un an, et alors tu auras une idée du télescope de tes rêves. Qu'en penses-tu ? Si tu as déjà eu cette expérience, dis-le nous, et dis-nous ce que tu en as conclu.

Je crois que Miaou a réalisé, cette nuit, en y réfléchissant, que le spectre sera déjà étroit à la base. Donc pas en faisant des observations.