Copyright (c) 2020 Jean-Pierre Prost.
La dispersion atmosphérique est une aberration introduite par l’atmosphère terrestre générant une déviation verticale des rayons lumineux en provenance de n’importe quel astre. Cette déviation est différente selon la longueur d’onde : ainsi, le rayonnement bleu est plus dévié que le rayonnement rouge, provoquant l’apparition d'un liseré rouge d’un côté de l'objet observé à l'oculaire et bleu de l’autre. En imagerie CCD, la résolution est également plus ou moins fortement dégradée et ce malgré l’utilisation de filtres de couleur à bande étroite.

Le Correcteur de Dispersion Atmosphérique (CDA en français ou ADC en anglais) est un dispositif optique basé sur un assemblage de prismes réglables, permettant de contrecarrer cette aberration.

Le phénomène de dispersion atmosphérique

Avant de parvenir au télescope, le rayonnement doit d'abord traverser l'atmosphère terrestre. Rentre alors en jeu le phénomène de réfraction, qui va agir sur ce rayonnement en le déviant à la manière du bâton "cassé" plongé dans l'eau. Le phénomène de réfraction est dû au changement du milieu de propagation de la lumière, depuis l'espace où règne le vide quasi absolu à l'atmosphère terrestre. Chaque milieu est caractérisé par son indice de propagation n.

Ce ne serait pas un problème en imagerie si cette déviation était homogène en longueur d’onde : dans ce cas, on n’observerait qu’un décalage global de l’image. Hélas, l’indice de l’atmosphère varie en fonction de la longueur d’onde.
La modélisation de l'indice atmosphérique a fait l'objet de nombreuses études. Celle de J.C Owens semble la plus répandue dans la littérature astronomique (voir notamment ici), étude qui a abouti aux équations suivantes :
formule dans laquelle :

      • Ds est le facteur de densité associé à l'air sec et qui est donné par la formule suivante :
      • Dw le facteur de densité associé à la vapeur d'eau et qui est donné par la formule suivante :
et avec les hypothèses suivantes :

      • Ps est la pression partielle de l'air sec. La valeur de Ps est reliée à l'altitude h (en mètres) par la relation : Ps = P0 *exp(- h / 7000), avec P0 = 1013,25 mb

      • Pw est la pression partielle de la vapeur d'eau. Cette pression est reliée à la température t (en Celsius) et l'hygrométrie (en %) par la formule suivante :
Les unités utilisées dans les formules sont : pression en millibars, longueur d'onde en microns, température en degrés Kelvin.

En se basant sur cette théorie, il est ainsi possible de tracer l'indice atmosphérique en fonction de la longueur d'onde du rayonnement :
avec les paramètres atmosphériques suivants :

      • t = 15°C

      • h = 150 m

      • Hygrométrie = 50%

On constate une plus forte variabilité dans le bleu que dans le rouge (la pente de variation de l'indice est plus fort pour les courtes longueur d'onde). La couche bleue pâtira donc le plus de ce phénomène. Pour nous astronomes, il en résulte à l'oculaire ou en photographie un décalage des couches de couleur se traduisant par un liseré rouge d'un côté de la planète et bleu de l'autre.

Ce phénomène est d'autant plus important que l'angle entre la direction du rayonnement et la normale à la couche atmosphérique est grand ... donc pour des objets à faible élévation.

Ce problème peut en partie être résolu en imagerie en recalant les couches rouge, verte et bleue : soit lors du compositage RGB pour un capteur N&B avec filtres interférentiels, soit par décomposition RGB/recalage par logiciel/recomposition pour des capteurs couleur.

En partie seulement car la dispersion atmosphérique intra-bande elle, n'est pas corrigée : et cette dispersion peut être conséquente notamment pour un filtre bleu. Cette dispersion intra-bande va générer une mauvaise qualité de l'image associée, qui peut être assimilée à un flouté généralisé. Par ailleurs, pas question non plus dans ces conditions de faire des images de luminance avec un capteur N&B en exploitant au maximum les possibilités de son télescope. A titre d'exemple, voilà pour des filtres de la marque Astronomik une simulation de son effet en fonction de l'élévation en utilisant le modèle présenté ci-dessus :
Le tableau suivant fournit pour différents diamètres d’instrument et ces 4 filtres LRVB, les valeurs d’élévation au-dessus desquels la dispersion dépasse la résolution du télescope utilisé (en utilisant le critère de Dawes 1.02 lambda / D )
Certes, dans la majorité des cas, la turbulence empêche de toutes façons d'utiliser son télescope jusqu'à à son pouvoir de résolution, problème bien plus important et limitant que ce phénomène de dispersion atmosphérique. Mais pour les quelques nuits de faible turbulence qui sont autant d'occasions à ne surtout pas rater, la dispersion risque de devenir le facteur majorant et dans certains cas très majorant, alors même qu'il existe des moyens de la compenser (voir plus bas). Par ailleurs, pour les luminances (pour du LRGB) la dispersion atteint des niveaux proches de la turbulence pour des élévations assez élevées : 1'' d'arc de dispersion sont atteint pour 53° d'élévation ! La correction de la dispersion permet ainsi d'exploiter à fond le LRGB quasiment toutes les nuits.


Application aux observations planétaires

En utilisant le graphe précédent, on voit que dans le cas de Jupiter, avec une élévation maximale de 25° environ (ce qui est le cas en 2020) la dispersion intra-bande dans le Rouge atteint environ 0.43 seconde d'arc ce qui correspond à la résolution d'un télescope de 260mm ! Dans le Vert, cette dispersion atteint 0.7 seconde d'arc, 1.7 secondes d'arc dans le Bleu et 2.7 secondes d'arc pour une Luminance. Ces dernières valeurs sont particulièrement élevées et montrent bien l'effet destructeur de la dispersion en termes de résolution instrumentale.

Par malheur, pour Jupiter ces conditions médiocres de visibilité dans l'hémisphère Nord vont perdurer jusqu'en 2022. Le graphe ci-dessous fournit les élévations maximales par nuit jusqu'en 2030 pourune latitude d'observation égale à celle de Nice (c'est dans cette région que j'observe !)
Pour Saturne, l'élévation maximale restera relativement faible jusqu'en 2026 environ, date à laquelle la planète dépassera les 50 d'élévation.
Enfin, pour Mars le graphe prend l'allure suivante (avec ajout sur le graphique du diamètre maximal en secondes d'arc). La situation de Mars est donc assez favorable jusqu'en 2029 soit 5 oppositions durant lesquelles la dispersion ne devrait pas être trop pénalisante.

Le correcteur de dispersion atmosphérique (ou ADC = Atmospheric Dispersion Corrector)

Les études menées depuis plusieurs années sur le phénomène de dispersion atmosphérique et les manières de la compenser ont montré que le décalage chromatique induit pouvait au 1er ordre être corrigé par l’utilisation de prismes en verre. Malheureusement, il n’existe aucun verre ayant un profil d’indice identique à celui de l’atmosphère sur une grande plage de longueur d’onde. Certaines combinaisons peuvent cependant apporter une correction tout à fait satisfaisante sur une plage plus réduite (typiquement 350 - 900 nm), ce qui suffit largement pour des applications amateurs : nos capteurs CCD ne sont de toutes façons que peu ou pas sensibles en dehors de cette plage.

2 types de combinaisons de prismes sont principalement utilisés :

      • 1 paire de prismes simples, contra-rotatifs et taillés dans le même verre (dits prismes de Risley). Le 1er prisme dévie et disperse de manière classique la lumière, le 2e prisme se chargeant de la ramener plus ou moins dans l’autre sens selon l’angle qu’il fait avec le 1er prisme :
L’avantage de cette solution est sa grande simplicité : seuls 2 prismes sont à fabriquer et le système contra-rotatif est facile à mettre en place. Voilà un exemple de tels prismes:
Ce système a cependant l’inconvénient majeur d’introduire une déviation latérale des rayons lumineux même en position 0. Lors du réglage en rotation des prismes, cette particularité provoque par exemple un mouvement important de l’objet photographié ou observé. Au cours du réglage du correcteur il faut donc recadrer systématiquement l’image.


    • 1 paire de prismes de type Amici. Cette configuration est similaire à la précédente, mais au lieu d’avoir de simples prismes, on utilise ici un assemblage de 2 prismes taillés dans des verres d’indices différents.
Cette solution permet d’éviter la déviation latérale précédemment évoquée. En revanche, la multiplication des éléments en verre qu’elle implique, entraîne une moins bonne transmission de la lumière, notamment dans l’UV domaine où la plupart des verres ont une mauvaise transparence.


Pour les correcteurs utilisés dans les grands observatoires (La Silla, Kitt Peak, …) l’absence de déviation revêt une importance particulière de part les mesures très pointues et précises qui y sont faites : c’est donc la 2e configuration Amici qui est utilisée.

En revanche, pour les correcteurs proposés sur le marché amateur, les prismes de Risley sont privilégiés afin de garder un système simple à fabriquer et à utiliser et maintenir des coûts suffisamment bas. Depuis quelques années, beaucoup de différents modèles de très bonne qualité sont commercialisés avec des prismes ayant généralement des angles entre 2 et 8°.

Apportons au passage une petite précision concernant cet angle de prisme. C'est une sorce d'ambiguïté car il peut s’agir de 2 angles différents :
      • soit l’angle au sommet du prisme (angle alpha dans le schéma ci-dessous),
      • soit l’angle de déviation du prisme (angle beta)
Le lien entre les deux dépend de l’indice du verre utilisé et de la longueur d’onde. En général, lorsque aucune précision n’est apportée, c’est qu’il s’agit de l’angle de déviation beta.
Parmi les multiples ADC disponibles citons:

      • le correcteur Astro Systems Holland (ASH) qui inclut 2 prismes de 4° d'angle beta, installés dansun carénage avec 2 molettes permettant la rotation différentielle et le réglage de l'ADC. Cet ADC est séparable en différents composants permettant différentes configurations de montage en fonction des chemins optiques voulus:
      • le correcteur Pierro Astro équipé de prismes à 2.5° d'angle dans sa version MK3. Dans cette version, les molettes ont été remplacée par un seul bouton permettant de régler l'écartement des prismes beaucoup plus simplement que pour les ADC classiques à molettes et indépendemment du réglage de l'horizontalité. Par ailleurs, la qualité optique de cet ADC est plus élevée que celle de ses concurrents,  notamment avec des prismes en silice fondue et un traitement anti-reflet particulier permettant une parfaite transmission jusque dans l'UV. Enfin, là aussi, l'ADC est morcellable pour plus de flexibilité dans les montages,
      • l'ADC de chez ZWO dont le design est similaire à celui d'ASH avec des prismes de 2° d'angle. Cet ADC incopore un niveau à bulle et une couronne graduée permettant de mieux repérer l'axe vertical local et de mieux symétriser l'écartement des molettes pour obtenir une correction parfaite de la dispersion.

Analyse du correcteur

L'analyse suivante a été faite pour un ADC utilisant des prismes en BK7, ce qui est le cas de la grande majorité des ADC disponibles à l'exception du MK3 de Pierro Astro. L’indice du BK7 varie en fonction de la longueur d’onde selon la courbe suivante:
Si les prismes de Risley du correcteur sont disposés en configuration 1 décrite ci-dessus, pour un angle quelconque séparant les 2 prismes, on obtient la figure suivante et les formules associées de Snell-Descartes :
Sur ce schéma, le trièdre X0Y0Z0 est fixe et relié au corps du correcteur, alors que le trièdre XYZ0 est lui lié au 1er prisme et donc tourne avec lui selon un angle delta par rapport à X0Y0Z0. Le 2e prisme effectue une rotation inverse d’un angle - delta, ce qui signifie donc que les 2 prismes sont séparés d’un angle 2 * delta.

Le calcul du vecteur de sortie R4 montre également une propriété intéressante du correcteur : quelque soit l’angle delta et l’indice n, R4 est toujours dans le plan (Y0,Z0), ou en d’autres termes sa composante selon X0 est nulle. En orientant le correcteur afin que X0 soit à l’horizontale, on peut ainsi corriger la dispersion verticale engendrée par l’atmosphère en effectuant une rotation symétrique des prismes et ce sans avoir à tourner le corps du correcteur.

Les formules permettent de calculer la déviation i4 générée par les prismes pour une longueur d’onde donnée. En effectuant ce calcul pour 2 longueurs d’onde, on obtient ainsi la dispersion générée par le correcteur.

Cette dispersion doit compenser celle de l’atmosphère. L’efficacité du correcteur est fonction de son positionnement par rapport au plan focal ainsi que de la longueur focale du système. Le schéma ci-dessous explicite cette relation :
On peut constater ainsi que pour une dispersion atmosphérique donnée, plus le correcteur sera près du plan focal, plus sa correction devra être importante ie plus l’angleentre les molettes devra être fort.

La relation entre les dispersions atmosphérique et du correcteur est la suivante

Dispersion correcteur requise = Dispersion atmosphérique * ( Focale / Ladc - 1)

Sur la base de ces calculs, on peut tracer les courbes fournissant la correction apportée par l’ADC en fonction de la rotation des prismes :

Ces courbes sont basées sur les hypothèses suivantes :

      • largeur de bande des filtres RGB Astronomik,

      • une longueur focale de 6600 mm,

      • une distance entre correcteur et plan focal de 45 mm, ce qui correspond à un montage assez serré.
Utilisation du Correcteur de Dispersion Atmosphérique (CDA)


En préliminaire, rappelons que le CDA ne corrige que les effets chromatiques induits par la dispersion atmosphérique mais pas les aberrations chromatiques générées par les lentilles des lunettes, des oculaires ou des barlows.

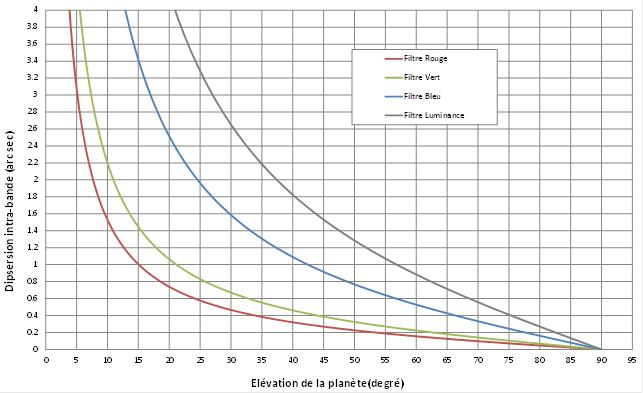
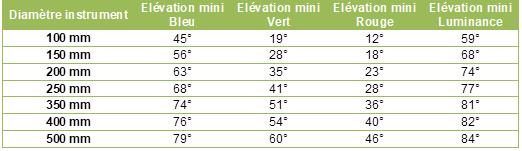
L’efficacité du correcteur est fonction notamment de sa distance au plan focal. Pour une dispersion atmosphérique donnée (donc pour une élévation de l’objet observé donné) plus le correcteur sera près du plan focal et plus la correction à réaliser par le CDA devra être importante c’est-à-dire plus il faudra augmenter l’angle entre les 2 prismes et donc plus il faudra écarter les molettes. On aura donc intérêt à rapprocher le CDA au maximum du plan focal pour avoir suffisamment de précision dans les réglages, tout en le gardant suffisamment loin pour rester dans sa gamme de correction possible.
Dans la pratique, la mise en place et l’utilisation du CDA se font selon les étapes successives suivantes :

1. le correcteur ne doit être utilisé qu'avec des rapports F/D assez importants, supérieurs à 10. Il doit donc le plus souvent être placé après la barlow. Dans le cas contraire, le correcteur introduit de l’astigmatisme. Par ailleurs, comme mentionné précédemment, ce positionnement permet de garder le CDA suffisamment près du plan focal. Le positionnement de la roue à filtre (si elle est utilisée) n’importe pas, mais là aussi on pourra jouer sur son positionnement relatif au CDA pour écarter plus ou moins ce dernier du plan focal,

2. les molettes du correcteur en position 0 (c’est à dire les deux molettes jointes) doivent être placées à l'horizontale une fois l'objet pointé afin de générer une dispersion dans la même direction que la dispersion atmosphérique. 2 positions sont possibles : mollettes à gauche ou à droite, mais une seule position permet d'effectuer les corrections dans le bon sens, l'autre au contraire l'amplifiant. Avec le montage optique sans renvoi coudé utilisé la plupart du temps et présenté sur la figure 2, les molettes doivent être positionnées à droite,

3. Si l’imagerie de l’astre est au programme, la caméra utilisée doit alors être mise en place à ce moment de la procédure. La mise au point est alors effectuée à l’aide de la caméra, du porte-oculaire et de l’ordinateur comme pour une classique séance d’imagerie. S’il s’agit d’une observation visuelle, cette étape peut être sautée ainsi que la suivante,
4. La caméra est alors retirée et remplacée par un oculaire dont la focale permet de clairement distinguer la dispersion : un grossissement de 1x à 1.5 le diamètre de l’instrument est conseillé, La mise au point doit être faite en coulissant l’oculaire dans le porte-oculaire mais sans toucher au dispositif habituel (porte-oculaire ou système de translation des miroirs). Cette étape permet de conserver les réglages qui seront utilisés lors de la séance d’imagerie et donc d’optimiser la correction de la dispersion dans cette configuration,

5. La dispersion doit alors être corrigée en agissant sur les deux molettes du CDA et en contrôlant les effets à l’oculaire, mais en prenant garde de tourner les molettes symétriquement par rapport à un axe restant horizontal afin que la correction soit effectuée dans le plan vertical c’est-à-dire dans la même direction que la dispersion atmosphérique.

Lors de la correction, on doit voir les liserés rouge d’un côté et bleu de l’autre progressivement disparaître et l’image devenir plus blanche et nette. Le point de correction optimal est déterminé à l’œil ce qui ne présente pas de difficulté particulière avec un peu d’entraînement.

Une méthode possible est par exemple de sur-corriger par une trop grande rotation des molettes pour obtenir des liserés rouge et bleu similaires à ceux du point 0 mais inversés, et déterminer ensuite le point médian.

Pour les objets pour lesquels la dispersion n'est pas très évidente à voir (comme Mars compte tenu de sa couleur rouge prononcée), on peut plus facilement régler le CDA sur une étoile (blanche de préférence) située à une élévation équivalente. On voit très bien les effets de la dispersion sur les anneaux de diffraction.

Sur Jupiter, on peut aussi trouver le réglage optimal en cherchant à obtenir une couleur du limbe identique de part et d'autre de la planète. Cette méthode permet d'avoir un réglage très fin pour cette planète.

Le réglage du CDA à l’œil se fait sans filtre ou avec un filtre Ir-Cut afin de clairement visualiser les effets de la dispersion sur tout le spectre lumineux accessible à l’œil,

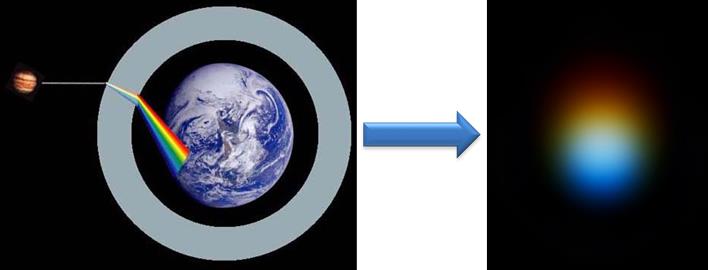
Une autre méthode de réglage du CDA fait appel à l’imagerie d’une étoile ou d’une planète de faible diamètre (Uranus ou Neptune par exemple) au travers d’un filtre violet W47. En effet, ce filtre laisse non seulement passer la lumière violette mais aussi l’infra-rouge. Or, comme expliqué précédemment, les effets de la dispersion atmosphérique varient en fonction de la longueur d’onde. Avec le filtre W47 on va donc pouvoir observer ses effets aux deux bouts du spectre.
En l’absence de correction avec un CDA, l’image de l’étoile se présente alors sous la forme de 2 spots séparés : l’un correspond à l’étoile vue dans le violet et l’autre à l’étoile vue dans l’infra-rouge. En tournant les molettes du CDA de manière symétrique, les 2 spots vont se rapprocher jusqu’à fusionner : en ce point, le réglage du CDA et la correction de la dispersion sont optimaux.
Pour cette méthode, l’utilisation d’une caméra numérique est requise puisque l’œil humain n’est pas sensible à l’infra-rouge.
La figure suivante fournit un exemple de ce type de réglage fait sur une étoile.
Il est à noter que l’image fantôme infra-rouge n’est pas toujours évidente à percevoir. Le réglage du CDA est donc plus ardu qu’avec la méthode visuelle. Cette méthode sera donc à réserver aux objets peu lumineux pour lesquels le réglage en visuel est très difficile à réalliser.


6. La caméra peut être remise en place et la séance d’imagerie peut commencer une fois le CDA réglé,

7. Ne pas oublier de régulièrement retoucher en cours de nuit le réglage du CDA (orientation et écartement des molettes) au fur et à mesure de l’augmentation ou de la diminution de l’élévation de l’astre imagé, en reprenant depuis l’étape 4. Une retouche environ toutes les 15 minutes est habituellement suffisant.

Afin de faciliter les réglages, les modèles de correcteur sont souvent gradués, ce qui permet de vérifier que le positionnement des deux manettes est bien symétrique par rapport à l'horizontale. Il est à noter que pour le CDA Pierro-Astro, la graduation est proposée en option sous la forme d’une réglette graduée à installer sur le correcteur. Les graduations permettent d'étalonner une fois pour toutes le réglage en fonction de la hauteur de l'astre: de gauche à droite ci-dessous, l'ADC ASH, Pierro Astro et ZWO.
D'autre part, sur l’ADC ASH, la direction qui correspond à l'horizontale est matérialisée par la vis de fixation de l'oculaire ce qui rend l'alignement avec l'horizontale très facile. Du côté du CDA Pierro-Astro, les courses des deux molettes se recouvrent ce qui permet d’avoir une certaine latitude sur le réglage de l’horizontale sans avoir à tourner l’ensemble du montage optique installé derrière le CDA. Enfin sur le ZWO, un niveau à bulle indique l'horizontale et permet donc avec les graduations de correctement régler les molettes.
Copyright (c) 2020 Jean-Pierre Prost.