
with various telescopes:
Newtonian 450 mm f/5, Newtonian 300 mm f/7, Newtonian 250 f/8, Dall-Kirham 200 f/3-15, classic C8 f/2-10, classic C14 f/11, RC 500 f/3-8
a) 2× "long Barlow lens", f = - 142.3 mm:
The OSLO model is from Telescopes, Eyepieces, Astrograph by Smith, Ceraglio, Berry, 2012 :

The field curvature has a radius of 141.1 mm (opposite to the incoming light).
b) 2× Clavé, f = - 113.4 mm
A Barlow lens of this type was calculated by Maurice Paul in 1935 for a 54 mm diameter (ref : Revue d'Optique Théorique et Instrumentale - Mai 1935 - Page 188). Latter on, Jean Texereau asked Clavé company in Paris to manufacture this type of lens in 27 mm diameter (1955). This design (Clairaut aplanetic doublet) is corrected from spherical aberration and is intended to correct the coma of f/5 Newtonian telescop. Specifications have been scalled down by Serge Bertorello for a 25.1 mm diameter based on the original Maurice Paul paper (see : http://serge.bertorello.free.fr/optique/dispoagr/barlwmp.html)

c] 2× Clavé by Kinoptik 1995, f = - 113.4 mm
Clavé company was bought and taken over by Kinoptik in 1989. The following characteristics is the actual design of the Clavé Barlow as manufactured by Kinoptik in 1995. Kinoptik was then purchased by Astronomix un 2003, which went bankrup in 2013. The last products actually made by Clavé were sold in 2005.

We can see that the actual design of the Clavé Barlow is very close to the design extrapolated by Serge Bertorello from Maurice Paul paper. The resulting spot diagram simulations are virtually identical.
The OSLO model is from Telescopes, Eyepieces, Astrograph by Smith, Ceraglio, Berry, 2012.
The field curvature has a radius of 97.9 mm (opposite to the incoming light).
e) 4× telecentric Barlow:
The OSLO model is from Telescopes, Eyepieces, Astrograph by Smith, Ceraglio, Berry, 2012. Unfortunately, there is no way to check how this design compares to Televue or Siebert telecentric designs.
The field curvature has a radius of 49.6 mm (opposite to the incoming light). This is the smallest radius of curvature of all four Barlow lenses evaluated here.
Strelh ratio :

- The "long Barlow" and the telecentric 4× perform beautifully down to 350 nm
- Even for on-axis high resolution imaging, Barlow lenses do not like to be used away from their nominal magnification factors. Both Clavé and "long Barlow" are no longer diffraction limited when pushed to 3× instead of nominal 2×.
- Two stacked Barlow lens give better results than increasing magnification factor of a single Barlow lens. However, Strehl ratio severely decreases below 400 nm.
- It is clearly better to use a single Barlow lens designed for the expected magnification ratio.
- The triplet "Shorty" Barlow is limited to 0.94 Strelh ratio from 350 to 450 nm (this is still diffraction limited).
Flat field diffraction limited field :
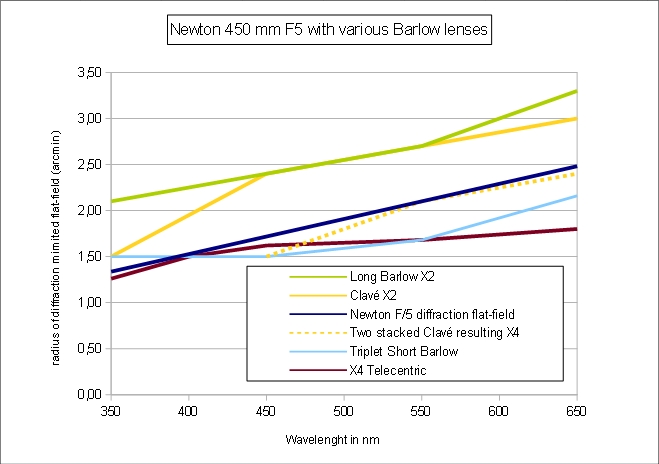
- The longer focal length Barlow lenses significantly expand the flat-field diffraction limited field (eg "long Barlow" and Clavé X2) while the short focal lenght ones decrease it (eg. Telecentric 4× which as a strong field curvature).
- The triplet "Shorty" Barlow is at no advantage compared to the "long Barlow" or the older Clavé.
There is virtually no LSA introduced by the "long barlow" at 2× factor (left). The reduction of the Strelh ratio at 3× is explained by the spherical aberration introduced by the Barlow lens at 3× (right)
LSA for 2× and 3× factors (450, 550 and 650 nm) :
Chromatic focal shift measured at the focus of Barlow at X2 factor :

The focusing being usually done by moving the Barlow lens and not the detector, the actual focal shift at the focuser is divided by ................;
2× Clavé Barlow lens and Newton 450 mm f/5
As designed, this Barlow lens shows a very small LSA at X2, which explains the high value of Strelh ratio. Increasing the magnification factor to 3× largely increases the LSA which explains the reduction of the Strelh ratio.
LSA are shown below for 2× and 3× factors (and 450, 550 and 650 nm) :

This old design compared well to the modern "long Barlow"using modern glasses with equivalent chromatic focal shift. The chromatic focal shift (here for 2× magnification) is very well contained from 400 to 800 nm. It becomes spectacular under 400 nm. To be checked for Venus UV imaging with a 100 nm bandwith filter ?

Strehl ratio and diffraction flat-field field :
LSA from 450, 550 and 650 nm. Chromatic focal shift from 300 to 800 nm.


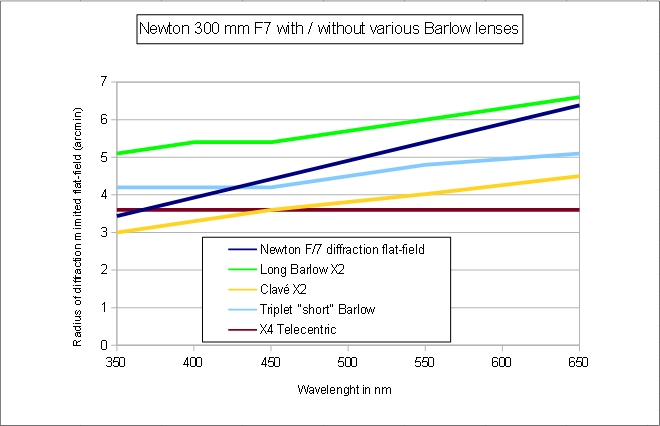
The "long Barlow" is still the top performer, while this time the triplet short Barlow gives a larger field than the older Clavé.
Strelh ratio :
- The Barlow lenses have an easy task at F/8, the Strehl ratio is equal to 1 for all wavelengths and Barlow lenses.
Flat-field diffraction limited field :

- This time, the "long Barlow" gives a much larger diffraction limited field than the other Barlow lenses. Still, this field is smaller than without the Barlow lenses
Performances of the "Long" Barlow lens with a DK 200 nm f/3-f/15 :
- No impact whatsoever on Strehl ratio nor diffraction limited flat field, probably because of the easy to deal native long F/15 ratio.
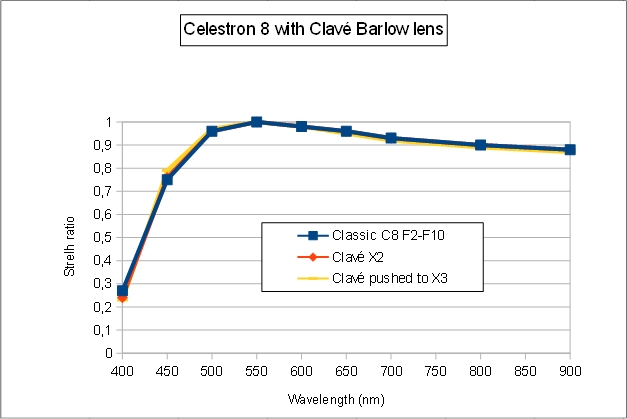

- At f/10, there is no impact of the Clavé Barlow lens on the Strehl ratio.
- The diffraction limited field is slightly increased by the use of Clavé Barlow (+25% in red light)

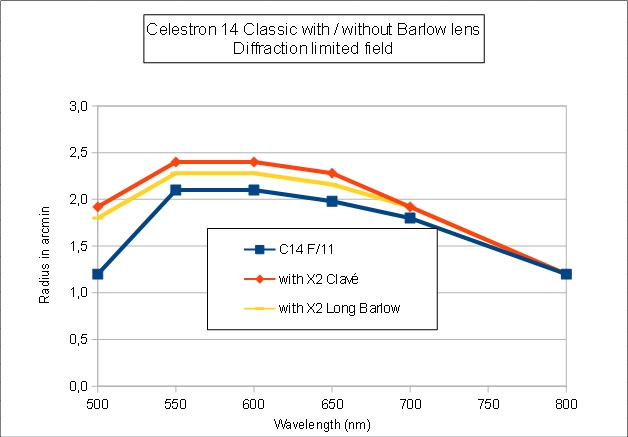
- Both Barlow lenses have no impact on the Strehl ratio.
- Both Barlow lens slightly increase the diffraction limited field.
- The "2× long Barlow lens" is clearly the best overall performer when it comes to Strehl ratio versus wavelength range and radius of the diffraction limited flat-field.
- The triplet Shorty design is at no advantage compared to the longer doublet design.
- While having excellent on-axis performance, the Telecentrix 4× design introduces strong field curvature which reduces the size of the diffraction limited flat-field..
- Depending on telescope design, the Barlow lens may increase or decrease the diffraction limited flat field (compared to "without Barlow").
- Barlow lenses have more difficult time at low f- ratio (e.g. f/5) and easier time at long ratio (e.g. f/8).
- Barlow lenses introduce a various amount of spherical aberration depending on their design.
- Even for on axis high resolution imaging, Barlow lenses do not like to be taken away from their nominal magnification factors (eg. 3× instead of 2×) because of increasing spherical aberrations and astigmatism.
- Barlow lenses introduce achromatic focal shift to be corrected by refocusing, specially in blue light.
- Barlow lenses introduce fieldl curvature opposite to the incoming light which could offset the field curvature of the instrument (generally concave to the incoming light).
- Coma correcting Barlow lenses such as APM 2.7× ED looks very promising for Newtonian telescopes.
Back to comparison of telescope optical designs for high resolution imaging