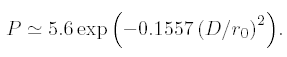
Turbulence is a real limiting factor in High Resolution Astronomy. A 250 mm
telescope is intrinsically able to provide a resolution of 0.5 arsec: this resolution
cannot be reached because of the atmosphere turbulence, that behaves like time-varying
random phase screen, destroying the image, like a bad shaped mirror.
The entrance pupil of a telescope located outside the earth's atmosphere, sees
a perfect plane wavefront. At the ground level, this plane wavefront is phase
distorted : this phase distortion could be expressed in microns (or Lambda=0.55µm
divided by something) for visible
light, as a "peak to valley" or rms distortion.
The way to reduce the turbulence effect is to reduce the exposure time, if the brightness of the object allows, so that it freezes the atmospheric turbulence. The webcam users have used this method for years now, allowing them to get outstanding images, called the "lucky exposure" method. The webcam allows nice frame rate (up to 30 frames per seconds), with resolution up to 640x480 pixels, for a very cheap price.
This setup can be used for funny experiments :
D.L Fried found an interesting property of the atmosphere : the coherence length
ro (diameter, not a radius) :
Ro can be defined as the diameter of a wavefront area over which the rms phase
variations due to atmosphere turbulence are equal to 1 rad (Lambda/6.28). The
ro parameter is a very good way to assess seeing and has been widely used since.
This r0 parameter defines the observed seeing : 251 * Lambda / ro (ro in mm,
lambda in µm) For instance, a ro=100mm gives at Lambda=0.55µm a
seeing of 1.38 arcsec, a ro=305mm gives a seeing of 0.45 arsec. Good astronomical
sites, like Paranal Obs. can get ro up to 400mm (s=0.35 arcsec), whereas ro
from 40 to 80mm (s=3.5-1.5 arcsec) are typical values for most places.
Using a webcam, or a video system, the probability of obtaining a frame among many, compliant with Lambda/6.28 criteria, is [1] :
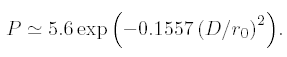
This formula is valid whenever D > 3.5 ro, in that case P is equal to one.
For instance a 305mm telescope, used under turbulence of ro=47mm (3 arcsec seeing) will provide a "good image" every 128 frames. To get all frames having wavefront distorsion not above Lambda/6.28 (i.e. 6.28 = 2*Pi), a ro=93mm is needed (i.e. a 1.48 arcsec seeing) using the same 305mm telescope. Nevertheless, the Lambda/6.28 is a tough criteria, and likely, good images can be achieved with wavefront distorsion from Lambda/4 to Lambda/3 rms.
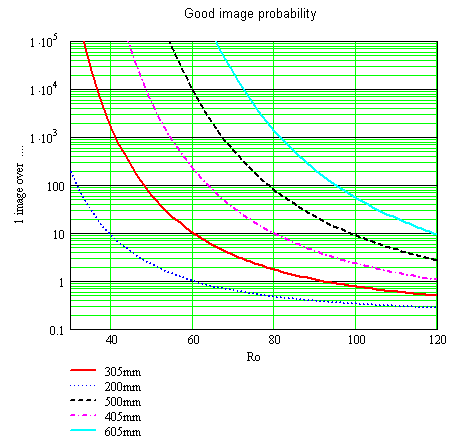
Amount of image to record in order to get Lambda/6.28 turbulence aberrations
versus Ro, for telescopes ranging from 200mm to 600mm
The next table provides the r0 max allowable for each Diameter, where in that case all images match the Fried criteria.
|
D |
r0 max |
|
605 |
172 |
|
500 |
142 |
|
405 |
115 |
| 305 | 87 |
| 200 | 57 |
As a sample, a part of a 300 frames sequence is shown here (figure 1), each exposure is 67ms (Vesta Pro Webcam). The pixel scale is 0.12 arcsec per pixel, recorded at the cassegrain focus of a qualified lambda/10 PTV, 305mm Schmidt cassegrain (focal length 9200 mm). The seeing has been judged as very mediocre by the owner of the telescope (the famous T.Legault). It easy to measure the seeing using this 20s sequence.

Figure 1
This is the image (below figure 2, same scale as top images) that should be recorded without turbulence. The FWHM is 0.45 arcsec.

Figure 2
The turbulence induces a fast shifting (figure 3) of the star : due to slopes distortion applied to the wavefront by the atmosphere.
It can be also measured, the next plot shows how the star has moved during
the 20s sequence :
- There is a slow motion, this is mainly due to the telescope mount tracking
error (these shifts will not be taken into account, and are actually small for
a pixel sampling of 0.12 arcsec)
- Turbulence induce star shifts, quick, the mean displacement is 0.64 arcsec
between two 66ms exposures.

Figure 3 : 20s sequence (300 frames, 66ms), the diamond symbol shows
the star centroid for a given frame.
If the image are stacked without reshift (image registration), the image exhibits
a 2.8 arcsec FWHM (vertical direction, figure 4), if the image are reshifted
and added (figure 5) the star FWHM is 2.3 arcsec, which is an improvement of
20% in term of resolution. This is anyway 5 time the resolution that can be
achieved with a 305mm telescope.
A formula provides r0, if an long exposure FWHM can be measured : Fwhm(rad)=0.98*Lambda/ro
With 2.8 arcsec, ro has been computed to 40 mm. Knowing ro, the seeing can be
estimated to 3.5 arcsec. With r0=40mm, 1 frame per 1958 will match the lambda/6.28
criteria.
 |
 |
 |
Figure 4 : simple stack |
Figure 5 : reshifted stack |
Figure 6 : best pick from 300 frame
sequence |
As a conclusion, the telescope diameter (main pupil size) has to be tailored with median seeing of your observing site.
Wavefront phase error, PSF
This section deals with software simulation. The turbulence effect can be simulated by degrading the entrance wavefront, and computing the star shape or PSF built by the telescope+wavefront. Zernikes polynoms have been used for this simulation. As shown hereafter, wavefront is the right circular shape (figure 6), the variation of image intensity within this disk shows (in Z) the wavefront phase shifts.
Very nice PSF can be calculated according the wavefront, provinding strhel ratios and L/... wavefront errors (ptv and rms)
This demonstrates quickly that Lambda/30 PTV mirrors are not really usefull
(!) Lambda/5-10 ptv mirrors are good enough, and more likely, the telescope
will never see calm an quiet turbulence conditions to be able to notice a difference
between a L/4 and L/30 mirror.

Figure 6 : perfect wavefront, purely diffraction limited, the right
circle shows the wavefront

Figure 7 : Turbulence effect - Lambda / 5.4 P-V wavefront error

Figure 8 : Turbulence effect - Lambda / 2.2 P-V wavefront error

Figure 9 : Turbulence effect - 1.4 * Lambda P-V wavefront

Figure 10 : Turbulence effect - 4.43 * Lambda P-V wavefront error

Figure 11 : Turbulence effect - 5.8 * Lambda P-V wavefront error
Software (written by myself).... that made the simulated PSFs and wavefronts.
Definitions :
FWHM : full width at half maximum : this is the diameter of the star when half of its maximum intensity is reached.
PTV or P-V : Peak to valley defect
PSF : point spread function, image of a star
Strehl Ratio : A ratio of the amount of light focused into disk center of the
Airy disk by a perfect optic (wavefront error = 0.0) versus an optic with aberrations
(wavefront error > 0.0). By definition, a diffraction limited telescope (including
central obstruction) focuses 68% of the incoming light into disk highest central
pixel. The maximum amount of light that can be focused by a perfect unobstructed
optic is 84% which is equal to a Strehl ratio of 1.00. Dividing 68% by 84% yields
a Strehl ratio of 0.80. An optical system with a Strehl ratio of 0.87 focuses
73% of the light energy. The higher the Strehl ratio the better the optic. The
Strehl ratio of a Newtonian telescope optical system can only be determined
via computer analysis of interferometric fringes or shack hartman sensors.
References :
[1] Diffraction-limited 800 nm imaging with the 2.56 m Nordic Optical Telescope
[2] Adaptive Optics: The Atmosphere
[3] Atmospheric Turbulence and its Effects on Image Formation
[4] The Intrinsic Seeing Quality at the WHT Site
[5] ESO presentation : Atmospheric turbulence in Astronomy by M.Sarazin (power point)
[6] Statistics of a Geometric Representation of Wavefront Distorsion D.L Fried (pdf)
[7] Probability of getting a lucky short-exposure image through turbulence D.L Fried (pdf)