 ETUDE
ETUDE  ETUDE
ETUDE Nous nous somme intéréssés
dans cette étude à la stabilité et à l'existence
de points placés à proximité de L4.
Comme nous l'avons vu précédemment, d'après l'étude
théorique, les 2 points L4 et L5 sont stables pour mu<0,038520897...
Dans un tel cas, un corps placé sans vitesse initiale à proximité de l'un de
ces points est attiré et décrit un mouvement de libration autour de celui-ci.
L'étude de la stabilité
est un domaine particulièrement vaste et il était nécessaire
de restreindre les conditions initiales afin de mener à bien une étude
réaliste et raisonnable.
Voici les conditions prises
pour l'étude:
En outre, nous avons utilisé la méthode de Runge-Kutta 4, plus adaptée à ce type d'étude. Nous avons fait un ajout au code de calcul de manière à obtenir une colonne supplémentaire dans le fichier de sortie représentant la distance (norme) de l'objet au point L4.
Les calculs ont été lancés de manière automatique par un script shell dont le code principal figure ci-dessous:
for coord in `seq 50 1` do
coordo=`puiss $coord 0.1 0.00001 50`
for compteur in `seq 1 200` do
mu=`puiss $compteur 0.5 0.00001 200`
echo '4' > troisC.in
echo $mu >> troisC.in
echo '100' >> troisC.in
echo '0.01' >> troisC.in
echo '1.0e-10' >> troisC.in
echo '1' >> troisC.in
echo $coordo >> troisC.in
echo $coordo >> troisC.in
echo '0.00' >> troisC.in
echo '0.00' >> troisC.in
echo '3.3' >> troisC.in
echo '0' >> troisC.in
troisC < troisC.in
norme=`tri`
touch F$coord.out
ligne=$mu' '$norme
echo $ligne >> F$coord.out
done
doneRemarques:
la fonction puiss fait appel à un petit programme en C permettant de renvoyer des valeurs selon une échelle logarithmique. Il admet 4 arguments;
Ainsi, >puiss 33 0.001 0.5 200 renvoie la valeur du 33ème éléments, sur un total de 200, répartis selon une échelle logarithmique (base10) entre 0.001 et 0.5;On se sert ici de 2 boucles FOR imbriquées, ou un fichier d'entrée différent troisC.in est créé à chaque boucle puis envoyé au programme de calcul principal.
La fonction tri est une petite fonction qui renvoie la valeur maxi de la norme pour un fichier de sortie donné.
 Les
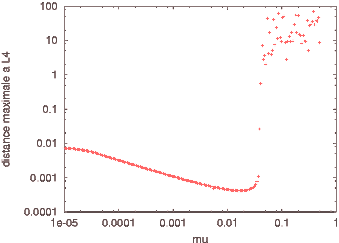
résultats sont les suivants: pour chaque valeur de distance initiale
au point L4, un fichier est créé, pour les 200 valeurs de mu,
avec la distance maxi atteinte par le troisième point. Ainsi, on peut
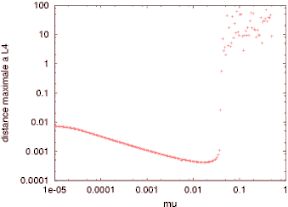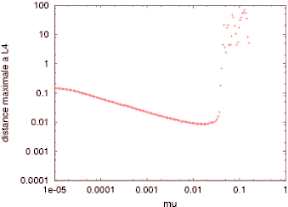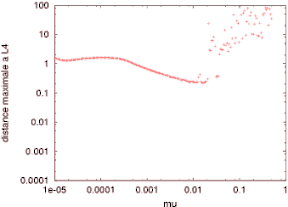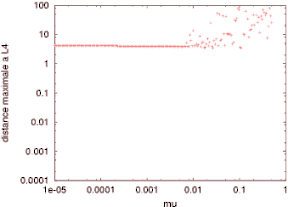
tracer un graphe comme celui ci-contre, avec, pour une distance de départ
donnée, en axe X: les différentes valeurs de mu, de 0.00001 à
0.5, et en axe Y: la distance maximale au point L4, atteinte en t=100.
Les
résultats sont les suivants: pour chaque valeur de distance initiale
au point L4, un fichier est créé, pour les 200 valeurs de mu,
avec la distance maxi atteinte par le troisième point. Ainsi, on peut
tracer un graphe comme celui ci-contre, avec, pour une distance de départ
donnée, en axe X: les différentes valeurs de mu, de 0.00001 à
0.5, et en axe Y: la distance maximale au point L4, atteinte en t=100.
On peut d'ores et déjà
constater sur cet exemple deux régimes bien distinct révélés
par l'étude: pour des valeurs de mu assez basses (comprises entre 1E-5
et environ 0.03), la distance au point L4 reste inférieure à 0.01
et son évolution est régulière. En revanche, lorsque mu
dépasse environ 0.03, la distance atteint des valeurs très élevées
(jusqu'à 100) et son évolution semble devenir chaotique.
On vient de mettre en évidence le phénomène d'instabilité
autour de L4 pour des valeurs de mu supérieures au mu-critique.
Partant de cette constatation, nous
avons décidé de rechercher si cette valeur de mu-critique pouvait
être approchée de manière empirique grâce au code
de calcul.
 Une comparaison
de différents paramètre de départ nous a permis de voir
que cette valeur de mu-critique pouvait être approchée si l'on
prenait une position de départ tres proche de L4.
Une comparaison
de différents paramètre de départ nous a permis de voir
que cette valeur de mu-critique pouvait être approchée si l'on
prenait une position de départ tres proche de L4.
Le graphe ci-contre le met bien en évidence de manière expérimentale:
lorsqu'on s'éloigne de L4 (rouge, vert, bleu, rose dans l'ordre), la
zone instable intervient pour des valeurs de mu de plus en plus petites, et
de manière moins "tranchée".
Cela a donc confirmé ce que nous pensions, et nous avons donc cherché
à approcher mu-critique en prenant une distance q1=q2=1E-6 (les autres
conditions restant inchangées).
Nous avons mené l'étude
en calculant 500 points répartis entre mu=0.015 et mu=0.045.
Comme attendu, nous constatons que
le troisième point s'éloigne plus de L4 à partir d'une
certaine valeur aux alentours de 0,037; il est important de préciser
que nous n'allons pas trouver la valeur exacte de mu-critique, mais plutot une
évaluation de la limite inférieure de sa valeur.
Sur le graphique ci-contre (échelle Log!), nous avons tracé la
variation de la norme (l'équivalent de la dérivée) lorsque
mu varie: on voit une augmentation très rapide (d'un rapport 100) autour
de 0,038. Nous pouvons donc affirmer que la valeur de mu-critique est faiblement
supérieure à 0,038.
Ce résultat est conforme à la théorie qui donne mu-critique
= 0,03852... (trait rouge) et nous sommes parvenus le retrouver de manière
expérimentale.
Tout d'abord, et afin de mieux comprendre le reste de l'étude, nous allons présenter ici différentes trajectoires du troisième point pour différents paramètres de départ, indiqués ci-dessous. On reste sans vitesse initiale, comme dans l'ensemble de l'étude.
|
Distance
de départ q1=q2=0.001
|
Distance
de départ q1=q2=0.00001
|
 |
 |
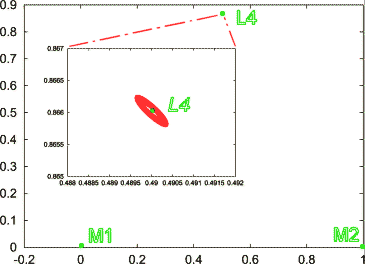
| t=1000, mu=0.0001: trajectoire assez "lache" et très allongée, mais régulière autour de L4. | t=1000, mu=0.0001: trajectoire très régulière, allongée et resserrée autour de L4 |
 |
 |
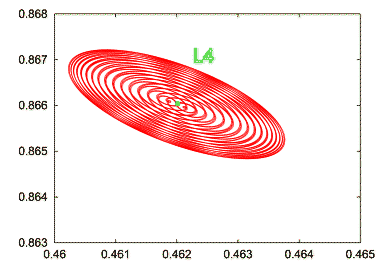
| t=1000, mu=0.001: trajectoire plus resserrée et plus arrondie autour de L4 | t=1000, mu=0.001: trajectoire encore très resserrée, régulière et arrondie autour de L4 |
 |
 |
| t=1000, mu=0.038: A l'approche du mu-critique, la trajectoire devient beaucoup plus large autour de L4 | t=1000, mu=0.038: malgrè le mu proche du mu-critique, la trajectoire est encore assez resserrée autour de L4. |
 |
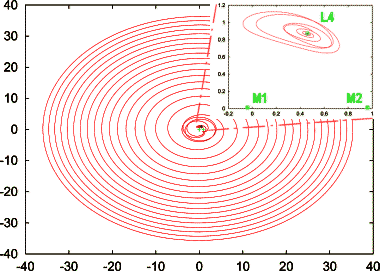 |
| t=100 (zoom) et 400 (gde image), mu=0.041: Le mu-critique a été dépassé: la trajectoire reste d'abord relativement proche de L4 (zoom), puis le point est soudain éjecté du système et s'éloigne régulièrement des deux autres masses en ligne droite (spirale dans le repère tournant) | t=100 (zoom) et 400 (gde image), mu=0.041: Le mu-critique a été dépassé: ici aussi, la trajectoire reste d'abord relativement proche de L4 (zoom), puis le point se retrouve également éjecté du système et s'éloigne régulièrement des deux autres masses en ligne droite (spirale dans le repère tournant) |
Conclusion: On remarque tout d'abord une différence pour mu<<mu-critique, selon la position du point au départ: lorsque le point est très proche de L4 (colonne de droite), la trajectoire reste très resserrée et régulière autour de L4, même lorsque mu augmente. Ainsi, si l'on souhaite une très grande stabilité spatiale (pour une sonde par exemple), on a intéret à la placer au plus proche de L4 (résultat qui parait assez logique).
En revanche, dès que mu dépasse mu-critique, l'étude met bien en évidence que le troisième point se retrouve éjecté systématiquement; de plus la position initiale n'intervient pratiquement plus sur le déroulement: le point est éjecté au bout d'un laps de temps sensiblement identique.
Nous exposons maintenant les résultats complets de l'étude: nous allons faire figurer sur un même graphe, de plusieurs manière différentes, l'évolution de la stabilité en faisant varier mu et la distance initiale. Nous avons donc besoin de réaliser un graphe 3D. Nous pouvons le faire de plusieurs manières différentes: soit un graphe 2D avec l'un des paramètres variant dans le temps (animation), soit un graphe 3D (3 axes).
 |
Voici ci-contre un graphe identique
à ceux présentés en haut de la page: |
On voit bien ici plusieurs choses intéressantes:
Afin d'avoir une vue plus synthétique du phénomène, il m'a paru interessant de réaliser un graphe 3D des données, avec:
 |
Ici, l'échelle de l'axe z (norme maxi) est une échelle décimale, mettant très bien en évidence l'existence de deux régimes:
|
 |
Ici, j'ai adopté une
échelle log sur l'axe des z (norme maxi). On voit mieux que là
zone où le point reste à proximité de L4 est assez
étendue, et on peut bien distinguer les limites de cette zone. Par exemple, on voit que le point reste à moins de 0.001 de L4 (zone bleu foncé), pour des valeurs de mu entre environ 0.001 et 0.01 et une distance initiale de environ 0.00001. |
 |
Un autre point de vue, mettant particulièrement bien en évidence la valeur de mu-critique et l'évolution de la zone critique selon la distance initiale.
|
A propos de l'étude:
Il est important de remarquer que nous avons dû limiter volontairement le cadre de l'étude. En effet, nous nous sommes limité à l'étude de la stabilité pour un temps t fixe et pour une position initiale dont la norme varie, mais avec q1=q2.
Ainsi, une étude exhaustive
aurait pu nécessiter un balayage de différentes positions tout
autour de L4, et pour des temps totaux variables.
On s'apperçoit vite que l'on se heurte à des difficultés
de représentations et qu'il faudrait des graphes 4D ou plus, ou bien
représenter l'information de manière partielle.
Suite:
Application - Les Troyens![]()