Page d'accueil Introduction Notion d'image Les critères Les défauts Tests visuels Test de Ronchi Foucault photo Foucault atelier >> Test de Roddier Contraste de phase Test du T460 Conclusion Bibliographie Liens |
|
|
|
|
Nous avons vu que lors des tests visuels (startests), on peut obtenir des informations sur les défauts optiques d'un instrument en observant deux images défocalisées d'une étoile. Le test de Roddier généralise ce concept en réalisant par logiciel une analyse photométrique et géométrique automatique des deux plages intra et extrafocales obtenues à l'aide d'un détecteur CCD.
- Le logiciel est disponible gratuitement sur le web.
- Voir l'avancement du projet et télécharger le logiciel WinRoddier.
Pour commencer, considérons un instrument parfait, donnant en son foyer limage dune étoile. On enregistre deux images défocalisée, lune à la distance l en avant du foyer, lautre à la même distance l en arrière du foyer.
La pupille dentrée est éclairée de manière uniforme (Intensité I0). Soit une petite portion de cette pupille (fig. 1) : le flux lumineux qui passe par cette petite portion éclaire limage intrafocale sur une surface plus petite, avec une intensité I1, et limage extrafocale sur une surface égale à celle de limage intrafocale, car les deux images sont à égale distance du foyer. Lintensité initiale I0 est donc « concentrée » de la même manière pour les deux images et on a :
I1 = I2
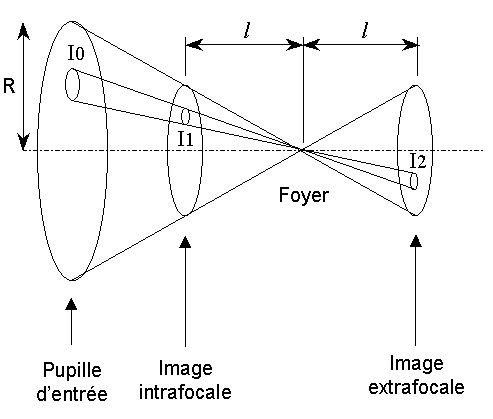
Fig. 1 : Test de Roddier avec un instrument
parfait.
Les intensités I1 et I2
sont égales.
Supposons maintenant que le front donde issu de la pupille dentrée ait un défaut : sur la petite surface de pupille considérée précédemment, il est incurvé (fig. 2). Le foyer réel est, pour cette portion de la pupille, situé en avant du foyer de linstrument. Sur limage intrafocale, la lumière est plus concentrée que sur limage extrafocale :
I1 > I2
Dans le test de Roddier, on compare donc I1 et I2,
grâce au calcul de la quantité
I2 I1, de manière à remonter
aux défauts du front donde .
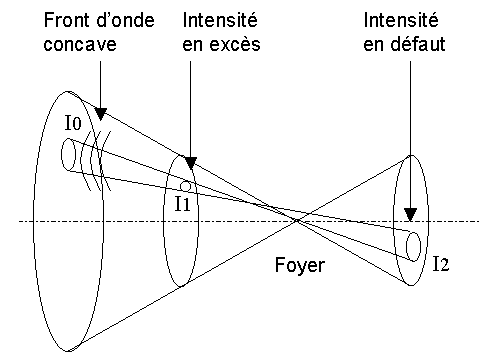
Fig. 2 : Test de Roddier avec un instrument
défectueux.
Les intensités I1 et I2
sont différentes. Cette différente d'intensité est
liée à la courbure du front d'onde.
La théorie montre que si l'on considère maintenant les images dans leur ensemble (et non des petites portions comme ci-dessus), le signal calculé en effectuant la soustraction des deux images intra et extra, est proportionnel au Laplacien du front d'onde.
- Le Laplacien du front d'onde, dont le calcul implique les dérivées secondes, est lié à la courbure de ce front d'onde( voir fig. 2). Le problème est ici inverse : il faut retrouver le front d'onde à partir de son Laplacien. Cela s'effectue à l'aide d'un logiciel spécialisé qui effectue en plus du calcul du Laplacien, de nombreuses corrections géométriques et photométriques visant à déterminer le front d'onde et ses aberrations.
|
|
2. Un exemple pour mieux comprendre
La figure 3 représente la région du foyer d' un instrument entaché de l'aberration de sphéricité (en sur-correction) : les rayons centraux convergent avec une distance focale plus courte que les rayons marginaux. Le front d'onde correspondant à cette aberration est traduit en niveaux de gris (fig. 4A) : le front d'onde est concave au centre et rabattu au bord. L'image de la figure 4B représente le Laplacien de ce front d'onde.

Fig. 3 : Région du Foyer d'un
instrument présentant une aberration de sphéricité
(sur-correction). Le bord de l'objectif a une distance focale plus longue
que son centre. Les signes + et - se réfèrent aux différences
d'intensité lumineuse sur les images intra et extra, par rapport
à une intensité uniformément répartie en l'absence
d'aberration (cas de la figure 1).
  |
  |
||||
|
|
|
Considérons maintenant les images intra et extra focales (fig. 5):
- Zone centrale des images : en intra il y a un excès d'intensité (noté +) et en extra il y a un défaut (noté -) car les rayons centraux convergent plus près de l'image intra (voir figure 3).
- Zone marginale des images : en intra il y a un défaut d'intensité (noté -) et en extra il y a un excès (noté +) car les rayons marginaux convergent plus près de l'image extra (voir figure 3).
- Zone centrale : Un excès d'intensité car (+) - (-) = (+)
- Zone marginale : Un défaut d'intensité car (-) - (+) = (-)
|
|
Une fois que l'on a reconstitué le front d'onde, on peut remonter aux valeurs des principales aberrations en décomposant ce front d'onde en polynomes de Zernike.
Ces polynomes sont des fonctions mathématiques définies sur un disque et qui peuvent être reliées aux principales aberrations. par exemple, l'image de la figure 4A est la représentation du polynome de Zernike qui est relié à l'aberration de sphéricité (lire plus de détails sur les polynomes de Zernike). En additionnant plusieurs polynomes, on peut reconstituer un front d'onde affecté d'autant d'aberrations. A l'inverse, un front d'onde mesuré peut être ajusté à plusieurs polynomes, de façon à "remonter" aux aberrations.
En guise d'exemple, nous reproduisons ici un extrait de l'analyse
d'un Schmidt-Cassegrain du commerce (de bonne qualité). La figure
5A est l'image du front d'onde renconstitué par le Logiciel EF à
partir de deux images intra et extra focales. Le tableau 1 donne les valeurs
rms de quelques aberrations et la figure 5B est l'image du front d'onde
reconstituée en utilisant les valeurs des aberrations et les
22 premiers polynomes de Zernike. L'utilisation de ces 22 polynômes
permet de retrouver les principales aberrations et de reconstruire la forme
générale du front d'onde.
  |
|
||||
|
|
